 por bruna106 » Sáb Abr 09, 2011 15:22
por bruna106 » Sáb Abr 09, 2011 15:22
Olá Boa Tarde
Estou tentando resolver um exercício mas o resultado não confere com o do livro. Se alguém puder me ajudar
eu ficarei muito grata.
**** A questão com a figura e resposta está em anexo ****
Para calcular o volume tentei fazer assim:
Limites:


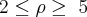


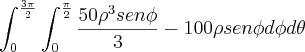


Parei por aqui pois quando substitui meus limites de phi notei que o resultado seria muito próximo de zero e conseqüentemente nÃo resultará no valor correto.
Não sei se meus limites estão errados ou se integrei algo errado. Alguém pode me ajudar por favor?
Muito Obrigada
- Anexos
-

-
bruna106
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Dom Abr 20, 2008 21:47
- Área/Curso: Estudante
- Andamento: cursando
 por LuizAquino » Seg Abr 11, 2011 11:04
por LuizAquino » Seg Abr 11, 2011 11:04
A casca esférica no exercício pode ser representada pela região em coordenadas esféricas:
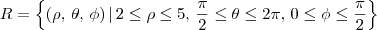
O volume dessa região será dada pela integral tripla (em coordenadas esféricas):
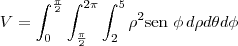
O exercício diz que a temperatura (em coordenadas esféricas) da região é dada por

(em graus Celsius).
Desse modo, a temperatura média sobre essa região será:
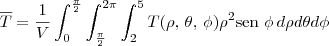
Agora, refaça o exercício considerando essas informações.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Coordenadas Esféricas] Integral Tripla
por raimundoocjr » Sáb Dez 14, 2013 00:22
- 0 Respostas
- 1663 Exibições
- Última mensagem por raimundoocjr

Sáb Dez 14, 2013 00:22
Cálculo: Limites, Derivadas e Integrais
-
- Integral tripla em coordenadas cilíndricas e esféricas
 por karllatorelli » Ter Jul 15, 2014 15:19
por karllatorelli » Ter Jul 15, 2014 15:19
- 0 Respostas
- 1129 Exibições
- Última mensagem por karllatorelli

Ter Jul 15, 2014 15:19
Cálculo: Limites, Derivadas e Integrais
-
- Coordenadas esféricas
por manuoliveira » Seg Jun 17, 2013 10:18
- 0 Respostas
- 1457 Exibições
- Última mensagem por manuoliveira

Seg Jun 17, 2013 10:18
Cálculo: Limites, Derivadas e Integrais
-
- Coordenadas esféricas
por Marcos_Mecatronica » Seg Jul 08, 2013 01:36
- 1 Respostas
- 1541 Exibições
- Última mensagem por young_jedi

Sex Jul 26, 2013 21:13
Geometria Analítica
-
- Sistemas de coordenadas esfericas
 por Jumarp » Sex Fev 25, 2011 22:58
por Jumarp » Sex Fev 25, 2011 22:58
- 4 Respostas
- 3117 Exibições
- Última mensagem por Jumarp

Dom Fev 27, 2011 12:37
Trigonometria
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


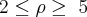


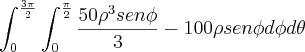




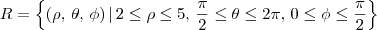
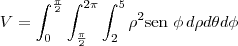
 (em graus Celsius).
(em graus Celsius).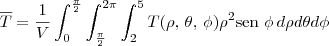

 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
