 por lucat28 » Sex Mar 18, 2011 14:47
por lucat28 » Sex Mar 18, 2011 14:47
Boa tarde senhores! To tendo dificudade em resolver a sequinte integral:
![\int_{}^{}\sqrt[]{x}Lnxdx \int_{}^{}\sqrt[]{x}Lnxdx](/latexrender/pictures/b59eb1fd4607bda6c41e48efd187337c.png)
A minha resposta é a seguinte:
![\frac{2}{3}\sqrt[]{{x}^{3}}(Lnx-\frac{2}{3})+c \frac{2}{3}\sqrt[]{{x}^{3}}(Lnx-\frac{2}{3})+c](/latexrender/pictures/b23f19e8f2027da2eb1109e249327859.png)
Sendo que a resposta que consta no gabarito é:
![\frac{2}{3} x \sqrt[]{x}Lnx-\frac{4}{9}x\sqrt[]{x}+c \frac{2}{3} x \sqrt[]{x}Lnx-\frac{4}{9}x\sqrt[]{x}+c](/latexrender/pictures/29aa335daa6b56ed0694fbb3a6c826c4.png)
então queria a ajuda de você pra achar o erro.
Desde já, obrigado!
-
lucat28
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Qua Mar 16, 2011 12:31
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia da Computação
- Andamento: cursando
 por lucat28 » Sex Mar 18, 2011 16:45
por lucat28 » Sex Mar 18, 2011 16:45
Muito obrigado Luiz...
não sei como deixei de enxergar isso, parece tão simples agora. Fiquei um tempão procurando o erro e não achava.
Valeu Luiz!
-
lucat28
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Qua Mar 16, 2011 12:31
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia da Computação
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Integral por partes - dúvida
por Danilo » Dom Nov 24, 2013 18:20
- 3 Respostas
- 1830 Exibições
- Última mensagem por e8group

Seg Nov 25, 2013 11:24
Cálculo: Limites, Derivadas e Integrais
-
- [Integral] Duvida na integração Por partes
por fabriel » Sáb Out 06, 2012 18:56
- 1 Respostas
- 1584 Exibições
- Última mensagem por MarceloFantini

Sáb Out 06, 2012 19:17
Cálculo: Limites, Derivadas e Integrais
-
- duvida na resolução da seguinte integral
por jmaracaipe » Seg Set 29, 2014 16:58
- 1 Respostas
- 1152 Exibições
- Última mensagem por jcmatematica

Ter Set 30, 2014 00:21
Cálculo: Limites, Derivadas e Integrais
-
- [INTEGRAL] Integral por partes! Alguem pode me ajudar?
por mih123 » Qua Jan 16, 2013 20:18
- 3 Respostas
- 4579 Exibições
- Última mensagem por adauto martins

Qua Out 22, 2014 09:11
Cálculo: Limites, Derivadas e Integrais
-
- integral por partes
por rita becher » Qua Jun 01, 2011 22:05
- 2 Respostas
- 2305 Exibições
- Última mensagem por rita becher

Qui Jun 02, 2011 10:30
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 6 visitantes
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 10:38
Olá ! Tenho essa dúvida e não consigo montar o problema para resolução:
Qual é o racional não nulo cujo o quadrado é igual à sua terça parte ?
Grata.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 12:27

Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 12:55
também pensei que fosse assim, mas a resposta é

.
Obrigada Fantini.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 13:01

Como

:

O que você fez?
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 16:17
eu só consegui fazer a igualdade, não consegui desenvolver o restante, não pensei em fatoração, mas agora entendi o que vc fez.
Obrigada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\int_{}^{}\sqrt[]{x}Lnxdx \int_{}^{}\sqrt[]{x}Lnxdx](/latexrender/pictures/b59eb1fd4607bda6c41e48efd187337c.png)
![\frac{2}{3}\sqrt[]{{x}^{3}}(Lnx-\frac{2}{3})+c \frac{2}{3}\sqrt[]{{x}^{3}}(Lnx-\frac{2}{3})+c](/latexrender/pictures/b23f19e8f2027da2eb1109e249327859.png)
![\frac{2}{3} x \sqrt[]{x}Lnx-\frac{4}{9}x\sqrt[]{x}+c \frac{2}{3} x \sqrt[]{x}Lnx-\frac{4}{9}x\sqrt[]{x}+c](/latexrender/pictures/29aa335daa6b56ed0694fbb3a6c826c4.png)

![\int_{}^{}\sqrt[]{x}Lnxdx \int_{}^{}\sqrt[]{x}Lnxdx](/latexrender/pictures/b59eb1fd4607bda6c41e48efd187337c.png)
![\frac{2}{3}\sqrt[]{{x}^{3}}(Lnx-\frac{2}{3})+c \frac{2}{3}\sqrt[]{{x}^{3}}(Lnx-\frac{2}{3})+c](/latexrender/pictures/b23f19e8f2027da2eb1109e249327859.png)
![\frac{2}{3} x \sqrt[]{x}Lnx-\frac{4}{9}x\sqrt[]{x}+c \frac{2}{3} x \sqrt[]{x}Lnx-\frac{4}{9}x\sqrt[]{x}+c](/latexrender/pictures/29aa335daa6b56ed0694fbb3a6c826c4.png)

![\frac{2}{3}\sqrt[]{{x}^{3}}\left(\ln x-\frac{2}{3}\right)+c = \frac{2}{3}\sqrt{{x}^{3}}\cdot (\ln x)- \frac{2}{3}\sqrt{{x}^{3}} \cdot \left(\frac{2}{3}\right)+c \frac{2}{3}\sqrt[]{{x}^{3}}\left(\ln x-\frac{2}{3}\right)+c = \frac{2}{3}\sqrt{{x}^{3}}\cdot (\ln x)- \frac{2}{3}\sqrt{{x}^{3}} \cdot \left(\frac{2}{3}\right)+c](/latexrender/pictures/4eeca4680946c4f0b0b5b76f412e7d55.png)

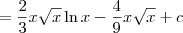
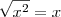 só pode ser feita pois no contexto dessa integral temos que x > 0.
só pode ser feita pois no contexto dessa integral temos que x > 0.


 .
.
 :
: