 por EulaCarrara » Ter Mar 15, 2011 16:50
por EulaCarrara » Ter Mar 15, 2011 16:50
Boa tarde!
Função dada:
![f(x,y)=\sqrt[2]{45-3{x}^{2}-5{y}^{2}} f(x,y)=\sqrt[2]{45-3{x}^{2}-5{y}^{2}}](/latexrender/pictures/0a4e1a3cc7aa77d3db28f7a5e62d9496.png)
Considerando Z=k (constante), me deparei com a seguinte equação:
Para k=0,
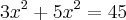
Para k=1,

...
Eis a dúvida.. as equações acima (das curvas de nível) são de uma circunferência ou de uma elipse (dividindo a equação por 45)?
E como x² e y² estão acompanhados de um número multiplicador, como chegar às curvas de nível?
-
EulaCarrara
- Usuário Ativo

-
- Mensagens: 19
- Registrado em: Seg Abr 19, 2010 21:21
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Zootecnia
- Andamento: cursando
 por LuizAquino » Ter Mar 15, 2011 17:44
por LuizAquino » Ter Mar 15, 2011 17:44
Temos a função
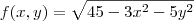
. Fazendo
z=k, ou seja,
f(x, y)=k, obtemos:
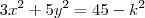
Lembrando que eu só pude fazer a simplificação

, pois temos que

para que o contradomínio da função seja o conjunto dos números reais, e não o dos números complexos. Em outras palavras, eu estou assumindo que não pode aparecer um número negativo dentro da raiz.
Agora, dividindo tudo por

e arrumando a equação:

Note que isso é uma elipse.
Recomendo que dê uma olhada no tópico:
[Dúvida]Gráficos de funções com duas variáveis.viewtopic.php?f=120&t=4069
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por EulaCarrara » Qua Mar 16, 2011 20:54
por EulaCarrara » Qua Mar 16, 2011 20:54
LuizAquino.. Obrigada!
Até aí entendi...
Mas no caso de se atribuir valores que está me confundindo..
Por exemplo, para
k=0:

Como seria esse desenho da elipse no esboço das curvas de nível?
-
EulaCarrara
- Usuário Ativo

-
- Mensagens: 19
- Registrado em: Seg Abr 19, 2010 21:21
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Zootecnia
- Andamento: cursando
 por LuizAquino » Qua Mar 16, 2011 23:14
por LuizAquino » Qua Mar 16, 2011 23:14
Há um vasto material na internet ensinando como esboçar o gráfico de uma elipse.
Com uma rápida pesquisa pelo Google, por exemplo, podemos achar a página:
Gráficos de Equaçõeshttp://www.dmm.im.ufrj.br/projeto/precalculo1/sala/conteudo/capitulos/cap31s4.html
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por EulaCarrara » Qui Mar 17, 2011 09:42
por EulaCarrara » Qui Mar 17, 2011 09:42
Sim... Eu dei uma olhada em vários sites... Só que todos os exemplos que eu encontrei, no denominador sempre tinha números quadrados perfeitos... No caso desse exercício que estou fazendo, "15" não tem raiz exata, por isso achei que teria algo diferente no esboço da curva..
De qualquer forma, obrigada!!

-
EulaCarrara
- Usuário Ativo

-
- Mensagens: 19
- Registrado em: Seg Abr 19, 2010 21:21
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Zootecnia
- Andamento: cursando
 por LuizAquino » Qui Mar 17, 2011 10:13
por LuizAquino » Qui Mar 17, 2011 10:13
Não há mistério algum. Basta calcular a raiz quadrada aproximada.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por EulaCarrara » Qui Mar 17, 2011 20:03
por EulaCarrara » Qui Mar 17, 2011 20:03
Ok ok!
O gráfico final foi um "semi" elipslóide invertido..
LuizAquino, muito obrigada *-*
Abraços!
-
EulaCarrara
- Usuário Ativo

-
- Mensagens: 19
- Registrado em: Seg Abr 19, 2010 21:21
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Zootecnia
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Dúvida]Gráficos de funções com duas variáveis.
 por Santa Lucci » Dom Mar 13, 2011 16:58
por Santa Lucci » Dom Mar 13, 2011 16:58
- 2 Respostas
- 2316 Exibições
- Última mensagem por Santa Lucci

Dom Mar 13, 2011 21:55
Cálculo: Limites, Derivadas e Integrais
-
- Funções de duas variáveis - Problemas (editado)
por Aprendiz2012 » Qui Set 20, 2012 12:48
- 1 Respostas
- 1450 Exibições
- Última mensagem por MarceloFantini

Qui Set 20, 2012 13:19
Funções
-
- [Limite de Funções de duas variáveis] Demostração
por ARCS » Dom Out 21, 2012 20:15
- 1 Respostas
- 2156 Exibições
- Última mensagem por MarceloFantini

Dom Out 21, 2012 22:04
Funções
-
- Máximos e mínimos de funções de duas variáveis
por Tathiclau » Qua Dez 11, 2013 23:22
- 0 Respostas
- 1071 Exibições
- Última mensagem por Tathiclau

Qua Dez 11, 2013 23:22
Cálculo: Limites, Derivadas e Integrais
-
- [Raiz Cúbica e Raiz Quadrada] Muito difícil achar a solução.
por Leocondeuba » Sáb Mai 11, 2013 19:27
- 2 Respostas
- 7453 Exibições
- Última mensagem por Leocondeuba

Sáb Mai 11, 2013 20:42
Aritmética
Usuários navegando neste fórum: Nenhum usuário registrado e 8 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![f(x,y)=\sqrt[2]{45-3{x}^{2}-5{y}^{2}} f(x,y)=\sqrt[2]{45-3{x}^{2}-5{y}^{2}}](/latexrender/pictures/0a4e1a3cc7aa77d3db28f7a5e62d9496.png)
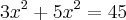



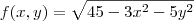 . Fazendo
. Fazendo 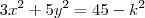
 , pois temos que
, pois temos que  para que o contradomínio da função seja o conjunto dos números reais, e não o dos números complexos. Em outras palavras, eu estou assumindo que não pode aparecer um número negativo dentro da raiz.
para que o contradomínio da função seja o conjunto dos números reais, e não o dos números complexos. Em outras palavras, eu estou assumindo que não pode aparecer um número negativo dentro da raiz. e arrumando a equação:
e arrumando a equação:


 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.