 por Moura » Qua Jan 19, 2011 23:02
por Moura » Qua Jan 19, 2011 23:02
Determine a derivada de y em relação a x:
![y=ln.\sqrt[]{\frac{(x+1)^5}{(x+2)^{20}}} y=ln.\sqrt[]{\frac{(x+1)^5}{(x+2)^{20}}}](/latexrender/pictures/f0c67dac0a4f591f99fcf6e8b6f2a566.png)
Resp.:
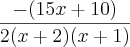
Desde já agradeço a ajuda.

P = NP
-
Moura
- Usuário Dedicado

-
- Mensagens: 41
- Registrado em: Seg Dez 13, 2010 11:14
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia da Computação
- Andamento: cursando
 por Elcioschin » Qui Jan 20, 2011 11:29
por Elcioschin » Qui Jan 20, 2011 11:29
V[(x + 1)^5] = (x + 1)^(5/2)
V[1/(x + 2)^20) = V[(x + 2)^-20] = (x + 2)^(-10)
y = ln[(x + 1)^(5/2)*(x + 2)^(-10)]
Lembre-se que:
a) Dx ln|u| = (1/u) Dx u
b) Dx (A*B) = B*Dx A + A*Dx B
u = [(x + 1)^(5/2)*(x + 2)^(-10)] ----> 1/u = (x + 2)^10/(x + 1)^(5/2)
Dx u = [(x + 2)^(-10)]*[(5/2)*(x + 1)^3/2] + [(x + 1)^(5/2)]*[-10*(x + 2)^(-11)]
Dx u = [5*(x + 1)^(3/2)]/[2*(x + 2)^10] - [10*(x + 1)^(5/2)]/[(x + 2)^11]
MMC = 2*(x + 2)^11
Dx u = {[5*(x + 1)^(3/2)]*(x + 2) - 20*(x + 1)^(5/2)}/2*(x + 2)^11
Colocando (x + 1)^(3/2) em evidência no numerador:
Dx u = [(x + 1)^(3/2)]*[5*(x + 2] - 20*(x + 1)]/2*(x + 2)^11
Dx u = [(x + 1)^(3/2)]*(- 15x - 10)/2*(x + 2)^11
Dx y = (1/u)*Dx u
Dx y = [(x + 2)^10/(x + 1)^(5/2)]* [(x + 1)^(3/2)]*(- 15x - 10)/2*(x + 2)^11
Dx y = - (15x + 10)/2*(x + 2)*(x + 1)
Ufa
-
Elcioschin
- Colaborador Voluntário

-
- Mensagens: 624
- Registrado em: Sáb Ago 01, 2009 10:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: formado
 por Moura » Qui Jan 20, 2011 21:00
por Moura » Qui Jan 20, 2011 21:00
P = NP
-
Moura
- Usuário Dedicado

-
- Mensagens: 41
- Registrado em: Seg Dez 13, 2010 11:14
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia da Computação
- Andamento: cursando
 por Elcioschin » Qui Jan 20, 2011 21:57
por Elcioschin » Qui Jan 20, 2011 21:57
Moura
Agradeço pelo Latex.
A apresentação ficou muito melhor.
Elcio
-
Elcioschin
- Colaborador Voluntário

-
- Mensagens: 624
- Registrado em: Sáb Ago 01, 2009 10:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Derivada de Logaritmo Natural] Exercício de logaritmo
por Ronaldobb » Dom Out 28, 2012 17:40
- 1 Respostas
- 2571 Exibições
- Última mensagem por MarceloFantini

Dom Out 28, 2012 18:16
Cálculo: Limites, Derivadas e Integrais
-
- Derivada de Logaritmo
por Moura » Qua Jan 12, 2011 14:41
- 1 Respostas
- 1530 Exibições
- Última mensagem por MarceloFantini

Qua Jan 12, 2011 15:00
Cálculo: Limites, Derivadas e Integrais
-
- Derivada de Logaritmo
por Moura » Qua Jan 12, 2011 22:35
- 1 Respostas
- 1429 Exibições
- Última mensagem por MarceloFantini

Qui Jan 13, 2011 11:13
Cálculo: Limites, Derivadas e Integrais
-
- Derivada de Logaritmo
por Moura » Qui Jan 13, 2011 14:47
- 1 Respostas
- 1491 Exibições
- Última mensagem por Elcioschin

Sex Jan 14, 2011 14:17
Cálculo: Limites, Derivadas e Integrais
-
- Derivada de Logaritmo
por Moura » Dom Jan 23, 2011 20:56
- 2 Respostas
- 1997 Exibições
- Última mensagem por Moura

Seg Jan 24, 2011 15:27
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 8 visitantes
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 10:38
Olá ! Tenho essa dúvida e não consigo montar o problema para resolução:
Qual é o racional não nulo cujo o quadrado é igual à sua terça parte ?
Grata.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 12:27

Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 12:55
também pensei que fosse assim, mas a resposta é

.
Obrigada Fantini.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 13:01

Como

:

O que você fez?
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 16:17
eu só consegui fazer a igualdade, não consegui desenvolver o restante, não pensei em fatoração, mas agora entendi o que vc fez.
Obrigada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![y=ln.\sqrt[]{\frac{(x+1)^5}{(x+2)^{20}}} y=ln.\sqrt[]{\frac{(x+1)^5}{(x+2)^{20}}}](/latexrender/pictures/f0c67dac0a4f591f99fcf6e8b6f2a566.png)
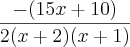


![y=ln.\sqrt[]{\frac{(x+1)^5}{(x+2)^{20}}} y=ln.\sqrt[]{\frac{(x+1)^5}{(x+2)^{20}}}](/latexrender/pictures/f0c67dac0a4f591f99fcf6e8b6f2a566.png)
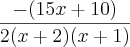






 .
.
 :
: