 por OtavioBonassi » Dom Jan 16, 2011 18:37
por OtavioBonassi » Dom Jan 16, 2011 18:37
"O valor de
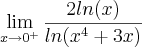
é :"
Como eu trabalho com ln 0 ? Tentei fazendo por L'Hopital ,mas nao é certo né, mas foi o unico jeito que eu imaginei de "sumir" com esse ln.Alguem tem alguma solução ?
-
OtavioBonassi
- Usuário Dedicado

-
- Mensagens: 38
- Registrado em: Qua Jan 05, 2011 14:57
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Mecatrônica
- Andamento: cursando
 por Cah » Dom Jan 30, 2011 21:13
por Cah » Dom Jan 30, 2011 21:13
Em uma sequencia de Fibonacci encontrei os valores {1,2,3,5,8,13,21,... } e agora tenho que demonstrar lim[(an+1)/an] = lim an/(an -1). Por favor, me ajude!!!
-
Cah
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Sáb Out 23, 2010 20:41
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matemática
- Andamento: formado
 por lucio Miranda » Seg Jan 31, 2011 17:46
por lucio Miranda » Seg Jan 31, 2011 17:46
vc coloca que b = lim(an + 1)/an = 1 + lim(an-1)/an = 1 + 1/lim an/(an - 1),
como a sucessão é crescente satisfaz a relação
bn = lim (an + 1)/an = lim an/(an - 1)
b*2 = b + 1
b*2 - b - 1 = 0
b = (1 +v5)/2
-
lucio Miranda
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Seg Jan 31, 2011 12:32
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
 por Cah » Seg Jan 31, 2011 18:46
por Cah » Seg Jan 31, 2011 18:46
OBRIGADA AJUDOU BASTANTE
-
Cah
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Sáb Out 23, 2010 20:41
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matemática
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Limite] Gráfico e limite para função maior inteiro
 por Raphaela_sf » Qui Abr 05, 2012 19:26
por Raphaela_sf » Qui Abr 05, 2012 19:26
- 1 Respostas
- 6642 Exibições
- Última mensagem por LuizAquino

Qui Abr 05, 2012 20:53
Cálculo: Limites, Derivadas e Integrais
-
- [Limite] Limite de funções reais de várias variáveis
por Bianca_R » Dom Nov 04, 2012 17:17
- 1 Respostas
- 4786 Exibições
- Última mensagem por MarceloFantini

Dom Nov 04, 2012 19:37
Cálculo: Limites, Derivadas e Integrais
-
- [Limite trigonométrico] Como calculo este limite?
por Ronaldobb » Qua Nov 07, 2012 23:14
- 3 Respostas
- 5118 Exibições
- Última mensagem por Ronaldobb

Qui Nov 08, 2012 07:37
Cálculo: Limites, Derivadas e Integrais
-
- [Limite] limite trigonométrico quando x tende ao infinito
por Ge_dutra » Seg Jan 28, 2013 10:13
- 2 Respostas
- 7257 Exibições
- Última mensagem por Ge_dutra

Ter Jan 29, 2013 14:20
Cálculo: Limites, Derivadas e Integrais
-
- [Limite] Limite de funções piso (maior inteiro)
por ViniciusAlmeida » Sáb Fev 14, 2015 10:09
- 2 Respostas
- 4434 Exibições
- Última mensagem por adauto martins

Qui Fev 19, 2015 15:01
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 7 visitantes
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 10:38
Olá ! Tenho essa dúvida e não consigo montar o problema para resolução:
Qual é o racional não nulo cujo o quadrado é igual à sua terça parte ?
Grata.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 12:27

Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 12:55
também pensei que fosse assim, mas a resposta é

.
Obrigada Fantini.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 13:01

Como

:

O que você fez?
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 16:17
eu só consegui fazer a igualdade, não consegui desenvolver o restante, não pensei em fatoração, mas agora entendi o que vc fez.
Obrigada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
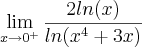 é :"
é :"
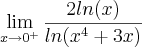 é :"
é :"




 .
.
 :
: