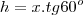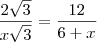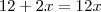Na figura abaixo, o triângulo ABC é equilátero com AM = MB = 4 cm e CD = 6 cm.

A área do triângulo CDE, em cm², é:
Alternativa certa:
A)
![\frac{18\sqrt[]{3}}{5} \frac{18\sqrt[]{3}}{5}](/latexrender/pictures/01d8b44244309325896e5af01a521759.png)
Eu tentei encontrar uma semelhança entre os dois triângulos de baixo, mas só tem um angulo congruente.
Outra dúvida se eu tiver as medidas do triangulo CDE, como encontro a área desse triãngulo? Pela formula Bxh/2 teria que ter a altura (h), certo! Aguardo ajuda, obrigado.