meus caros, saudações!
Assisti um vídeo do IMPA (um vídeo maravilhoso!) sobre construções geométricas... o Wagner desenhava com régua e compasso qualquer fórmula!
Ele demonstrou, algebricamente e geometricamente, que a média geometrica [x] de dois valores [a, b] é igual a ?ab.
Entretanto, ele também afirmou que a terceira proporcional é igual a média geométrica, ou seja: a/x=x/b <=> x=?ab.
Consultando o google e o site somatematica, notei que a definição de 3ª proporcional não é a/x=x/b <=> x=?ab como o wagner definiu, e sim: a/b=b/x => x=b²/a.
Como assim, é possível ter quantas interpretações para o conceito de 3ª proporcional?
Quem está certo, quem está errado??
agradeço os esclarecimento,
José h
, veja:
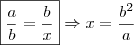
![\sqrt[]{ab} = \frac{b^2}{a} \\\\\\ \left( \sqrt[]{ab}\right)^2 = \left( \frac{b^2}{a}\right)^2 \\\\\\ ab = \frac{b^4}{a^2} \\\\ a^3b = b^4 \\\\ a^3 = b^3 \\\\ \boxed{\boxed{a = b}}](/latexrender/pictures/f2e2510ac94135e65e4cbef2bcf0c2ee.png "\sqrt[]{ab} = \frac{b^2}{a} \\\\\\ \left( \sqrt[]{ab}\right)^2 = \left( \frac{b^2}{a}\right)^2 \\\\\\ ab = \frac{b^4}{a^2} \\\\ a^3b = b^4 \\\\ a^3 = b^3 \\\\ \boxed{\boxed{a = b}}")
