 por Sal » Sáb Mar 17, 2012 16:33
por Sal » Sáb Mar 17, 2012 16:33
(UESPI-PI) Entre os pontos A e B de uma região plana passa um rio retilíneo com 20 m de largura. Um caminho constituído de estradas retilíneas e uma ponte sobre o rio devem ser construídos conectados os pontos A e B, A distância entre A e a margem do rio é de 30 m. e a distância entre B e a margem do rio é de 40 m. A ponte deve ser perpendicular às margens retilíneas do rio, como ilustra a seguir,
Qual o menor comprimento possível do caminho? Resposta correta 270 m.
Esta atividade esta relacionada no livro como semelhança de triângulos e estamos utilizando razões para sua resoluções. Dessa forma não conseguimos encontrar a solução e resolvemos pelo teorema de Pitágoras desconsiderando a ponte e o rio
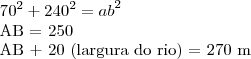
Gostaria de saber se posso considerar AB um segmento contínuo.
- Anexos
-

Editado pela última vez por
Sal em Dom Mar 18, 2012 11:10, em um total de 1 vez.
-
Sal
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Sáb Mar 10, 2012 10:55
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: regular
- Andamento: cursando
 por LuizAquino » Dom Mar 18, 2012 01:26
por LuizAquino » Dom Mar 18, 2012 01:26
Sal escreveu:(UESPI-PI) Entre os pontos A e B de uma região plana passa um rio retilíneo com 20 m de largura. Um caminho constituído de estradas retilíneas e uma ponte sobre o rio devem ser construídos conectados os pontos A e B, A distância entre A e a margem do rio é de 30 m. e a distância entre B e a margem do rio é de 40 m. A ponte deve ser perpendicular às margens retilíneas do rio, como ilustra a seguir,
Qual o menor comprimento possível do caminho? Resposta correta 270 m.

- ativ rio.jpg (27.66 KiB) Exibido 4242 vezes
Sal escreveu: Esta atividade esta relacionada no livro como semelhança de triângulos e estamos utilizando razões para sua resoluções. Dessa forma não conseguimos encontrar a solução e resolvemos pelo teorema de Pitágoras desconsiderando a ponte e o rio
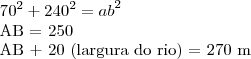
Gostaria de saber se posso considerar AB um segmento contínuo.
Você não pode (magicamente) desconsiderar o rio e a ponte, criando assim um triângulo retângulo de hipotenusa AB e de catetos 70 e 240. A não ser que você justifique porque isso pode ser feito.
O menor caminho será dado quando os dois triângulos retângulos AMC e BND forem semelhantes (vide a figura abaixo).
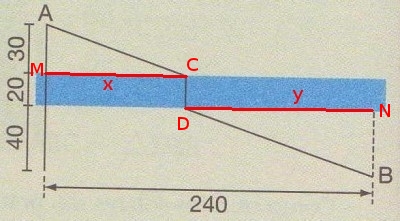
- ativ rio2.jpg (56.63 KiB) Exibido 4242 vezes
Podemos então montar o sistema:

Resolvendo esse sistema, obtemos que
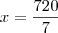
e
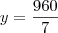
.
Temos então que:


O comprimento L do caminho será:
 Observação
ObservaçãoVocê provavelmente deve estar se perguntando: "mas por que a minha resolução deu certo?".
A sua resolução só deu certo, pois na figura os triângulos retângulos AMC e BND são semelhantes e as margens do rio são paralelas. Desse modo, como MC e ND são paralelos e AM e BN são paralelos, temos que AC e BD são paralelos. Deslocando BD paralelamente até que o ponto D encontre o ponto C, podemos formar um triângulo retângulo de hipotenusa AB e de catetos 70 e 240. Se você tivesse explicado isso, então a sua solução estaria correta.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Sal » Sáb Mar 24, 2012 19:43
por Sal » Sáb Mar 24, 2012 19:43
Ok, muito obrigada
-
Sal
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Sáb Mar 10, 2012 10:55
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: regular
- Andamento: cursando
Voltar para Geometria Plana
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Teorema de Tales e Semelhança
 por Sal » Sáb Mar 10, 2012 11:35
por Sal » Sáb Mar 10, 2012 11:35
- 2 Respostas
- 3744 Exibições
- Última mensagem por Sal

Dom Mar 11, 2012 14:46
Geometria Plana
-
- [Semelhança de triângulos] Triângulos quadrados
 por Debora Bruna » Seg Ago 08, 2016 12:18
por Debora Bruna » Seg Ago 08, 2016 12:18
- 0 Respostas
- 1473 Exibições
- Última mensagem por Debora Bruna

Seg Ago 08, 2016 12:18
Geometria Plana
-
- Teorema de Tales
por LuanRodrigues » Qua Mai 04, 2011 23:42
- 1 Respostas
- 2574 Exibições
- Última mensagem por FilipeCaceres

Qua Mai 04, 2011 23:46
Geometria Plana
-
- Teorema de Tales
 por LuanRodrigues » Qui Mai 05, 2011 21:26
por LuanRodrigues » Qui Mai 05, 2011 21:26
- 1 Respostas
- 4956 Exibições
- Última mensagem por Molina

Sex Mai 06, 2011 12:52
Geometria Analítica
-
- teorema de tales
 por bmachado » Seg Mar 26, 2012 17:51
por bmachado » Seg Mar 26, 2012 17:51
- 3 Respostas
- 2501 Exibições
- Última mensagem por ednaldo1982

Sex Mar 30, 2012 01:11
Geometria Plana
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
zig - Sex Set 23, 2011 13:57
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
Vennom - Sex Set 23, 2011 21:41
zig escreveu:![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Rpz, o negócio é o seguinte:
Quando você tem uma potência negativa, tu deve inverter a base dela. Por exemplo:

Então pense o seguinte: a fração geratriz de 0,05 é

, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
Veja:
![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
A raiz quadrada de vinte, você acha fácil, né?
Espero ter ajudado.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:23
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:24
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
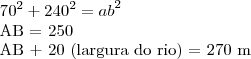



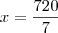 e
e 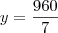 .
.



![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.