(Ufmg 2002) Na figura abaixo, a circunferência tem centro O e o seu raio tem a mesma medida do segmento BC. Sejam alfa a medida do ângulo AÔD e ’beta a medida do ângulo alfa e beta
nao consigo copiar e colar a figura...por favor me ajude.






alfabeta escreveu:(Ufmg) Na figura abaixo, a circunferência tem centro O e o seu raio tem a mesma medida do segmento BC. Sejam ? a medida do ângulo AÔD e ? a medida do ângulo ACD.
Ache ? em função de ?
alfabeta escreveu:Tentativa de resolução: primeiro, eu disse que o arco AD é igual a ?, que é o angulo central. ? é o angulo externo do triangulo AOB, portanto vale B mais OÂC. não sei como achar este último angulo.
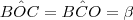 .
. .
.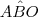 é externo ao triângulo OBC. Sendo assim, temos que
é externo ao triângulo OBC. Sendo assim, temos que 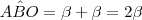 .
.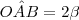 .
.

Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes