)=62° e m(
)=18°. Calcule a medidade do ângulo formado pela altura AH com a bissetriz AS (a questão não possui imagens).Tentativa de Resolução;
Tentei utilizar seno, cosseno e tangente dos ângulos depreendidos. Mas, não obtive êxito.
por raimundoocjr » Ter Fev 21, 2012 09:39
)=62° e m()=18°. Calcule a medidade do ângulo formado pela altura AH com a bissetriz AS (a questão não possui imagens).por MarceloFantini » Ter Fev 21, 2012 12:32
, onde as letras menores denotam os ângulos. Sabendo 
e 
, encontre 
. Agora, trace a bissetriz 
. Com isso, sabemos que o ângulo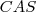 
é igual ao ângulo 
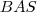e tem valor 
. Trace agora a altura 
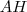que é perpendicular a 
. Então os ângulos 
e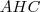 
são retos.. Temos um ângulo reto e outro de 62°, logo o outro é 28°. Sabemos então que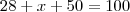 
onde x é o ângulo 
que procuramos, logo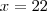 
. Outra forma é pelo triângulo 
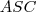, onde temos os ângulos de 50° e 18°, sobrando 112°. Como este é externo, lembrando o teorema que diz que o ângulo externo é soma dos outros dois ângulos do triângulo teremos 
, novamente a resposta.
por Arkanus Darondra » Ter Fev 21, 2012 12:54
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png "\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}")
![\sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png "\sqrt[]{2}")
(dica : igualar a expressão a 
e elevar ao quadrado os dois lados)