Olá Hugo.
Por favor, redija seus textos quando for postar. Apenas em imagens aquilo que for necessário.
Isso porque se o seu texto não estiver escrito, as pessoas não encontraram uma dúvida já sanada aqui no fórum por meio do mecanismo de busca.
J Hugo escreveu:De uma lâmina quadrada de metal corta-se uma peça circular do maior tamanho possível, e desta corta-se um quadrado, também do maior
tamanho possível. Se o lado do quadrado original mede 16 cm, a área da superfície do metal que foi desperdiçado, em centímetros quadrados, é:

A área desperdiçada é aquela que não foi usada para obter o quadrado JMNP (Verde)
Área do quadrado ABCD (Preto): 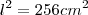 Área do quadrado JMNP (Verde):
Área do quadrado JMNP (Verde):Temos que sua diagonal (azul) vale
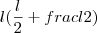
Por pitágoras, seu lado vale
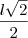
Sua área:

Então o desperdício foi de
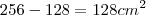
J Hugo escreveu:Se o hexágono regular da figura tem área 2, a área do pentágono assinalado é


Vemos que a área total do hexágono vale 6 área do triângulo destacado
Logo, a área do pentagono





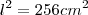
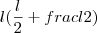
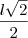

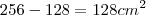






 , avisa que eu resolvo.
, avisa que eu resolvo.

