[Geometria Plana] Semelhança de Triângulos

por **vanessafey** » Sáb Ago 27, 2011 23:50

Olá, estou tentando resolver os exercícios do livro Dando Corda na Trigonometria, de Oscar Guelli e não consigo resolver o exercício 4 da página 25. Esbocei no paint a figura desejada. Já tentei de várias maneiras e não consigo chegar ao resultado do gabarito. Segue o problema:

Na figura, o segmento MN é paralelo à base do triângulo ABC. Decompondo a figura em em dois triângulos semelhantes, descubra o valor de x.

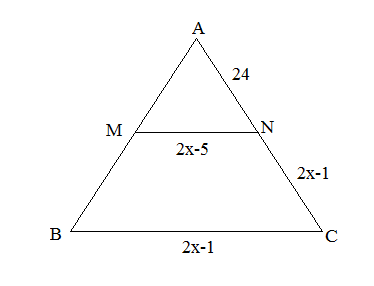
: triângulo.png (4.99 KiB) Exibido 8065 vezes

por **LuizAquino** » Dom Ago 28, 2011 00:01

Como os triângulos ABC e AMN são semelhantes, temos que:

$\frac{MN}{BC} = \frac{AN}{AC}$

Isso significa que temos a equação:

$\frac{2x-5}{2x-1} = \frac{24}{24 + (2x - 1)}$

Agora basta resolver a equação.

vanessafey escreveu:Esbocei no paint a figura desejada.

Que tal usar um programa mais adequado para esse trabalho?

Eu recomendo o GeoGebra, cujo a página oficial é:
http://www.geogebra.org

Se desejar um conjunto de vídeo tutoriais sobre esse programa, então veja se o meu canal pode ajudar:
http://www.youtube.com/LCMAquino

por **vanessafey** » Dom Ago 28, 2011 00:47

Ok! Não sei se estou errando nos cálculos, mas tbm estava com este raciocínio... Porém resolvendo esta equação em X, encontrei x=4 e depois x=97/2 e o livro traz como gabarito x=6,5

Não consegui ainda! Obrigada por enquanto!

por **LuizAquino** » Dom Ago 28, 2011 00:55

vanessafey escreveu:Não sei se estou errando nos cálculos, mas tbm estava com este raciocínio... Porém resolvendo esta equação em X, encontrei x=4 e depois x=97/2

Você está errando nos cálculos, pois as soluções da equação são x = -7/2 e x = 13/2. Obviamente descartamos a primeira solução, pois caso contrário os segmentos teriam comprimento negativo (o que não faz sentido).