Seguinte, estou tentando resolver um problema de geometria, mas não estou conseguindo obter o resultado correto!
O problema é o seguinte, a imagem é de um parque, existe um caminho que está na cor cinza. O problema quer saber a área desse caminho!
Eu fiz da seguinte maneira: calculei a área dos dois triângulos. Obtendo valor
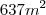 ,
,calculei o valor do parque todo, que no caso é o retângulo


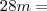
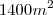
Somei as duas áreas dos triângulos

Então peguei a área do parque - a área dos triângulos, resultando
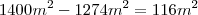
Sendo a área do caminho

Mas observei no final do livro a resposta, e não está correto! esse meu raciocínio está errado?






 , avisa que eu resolvo.
, avisa que eu resolvo.

