 por Caroline Oliveyra » Dom Jul 10, 2011 13:34
por Caroline Oliveyra » Dom Jul 10, 2011 13:34
Oi! [eu de novo

]
Tem um exrcício aki numa das minhas listas que pede para eu verificar que as equações dadas são de uma circunferência, achar o centro e o raio.
Eu sei que pra uma eq. representar uma circunferência ele deve se encaixar em três condições: os coeficientes de

e de
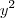
devem existir e devem ser iguais; não pode existir coeficiente para
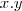
e
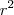
deve ser maior que 0. Na equação

eu achei o
centro (coeficiente de x
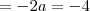
e coeficiente de
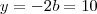
) mas não sei como achar o raio.
Eu tenho que passar essa equação para a forma reduzida? Eu não lebro se aprendi a fazer isso no ensino médio. Como posso demonstrar que essa eq. representa uma circunferência?
Na eq.
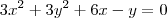
não tem nem termo independente, como se acha o raio disso?
MUITO obrigada desde já a quem puder me ajudar!!!
Grande beijo!

"... então não importa se você é antílope ou leão; amanheceu, comece a correr."
-
Caroline Oliveyra
- Usuário Ativo

-
- Mensagens: 23
- Registrado em: Dom Jun 19, 2011 13:35
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Metalúrgica e de Materiais
- Andamento: cursando
 por Caroline Oliveyra » Dom Jul 10, 2011 15:45
por Caroline Oliveyra » Dom Jul 10, 2011 15:45
Nuss, que confusão que eu fiz aqui... nem eu to entendendo mais o que eu postei... o.O'
Bom, eu já entendi o exercício em que eu estva em dúvida.
"... então não importa se você é antílope ou leão; amanheceu, comece a correr."
-
Caroline Oliveyra
- Usuário Ativo

-
- Mensagens: 23
- Registrado em: Dom Jun 19, 2011 13:35
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Metalúrgica e de Materiais
- Andamento: cursando
 por giulioaltoe » Dom Jul 10, 2011 21:21
por giulioaltoe » Dom Jul 10, 2011 21:21
caroline, acho que fica mais facil se voce tental analisar achando as possiveis multiplicaçoes da qual sairam os termos, se voce analisar primeiramente o termo elevado ao quadrado e os termos que apresentam x e fazer um produto notavel dele o termo que sobrar, ou seja oque voce nao analisou vai ser um numero solto, entao apos voce analisar o X e o Y, voce compensa a equação! ex:
x²-4x+y²+10y, sem prestar atenção no 13 uma possivel multiplicação seria (x-2)² = x²-4x+4 e (y+5)²= y²+10y+25, mas como a funcao inicial o termo C é 13 subeentende-se que o R=16 pois x²-4x+y²+10y+29=16 e quando se subtrai 16 dos dois lado para igualar a equação a 0 ela volta a equação inicial

na outra questao tem que fazer a mesma coisa.... analisar e depois ver quanto falta para zerar a função que vai ser o provavel R
ainda na lista 4?
-
giulioaltoe
- Usuário Dedicado

-
- Mensagens: 45
- Registrado em: Qui Jun 23, 2011 21:29
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia metalurgica e mat - UENF
- Andamento: cursando
 por Caroline Oliveyra » Ter Jul 12, 2011 14:25
por Caroline Oliveyra » Ter Jul 12, 2011 14:25
Ah, eu consegui fazer depois... kkkkkkkkkkkkkkkkkkkkkk Eu tava histérica quando postei!
Brigada assim mesmo XD
Bjo!
"... então não importa se você é antílope ou leão; amanheceu, comece a correr."
-
Caroline Oliveyra
- Usuário Ativo

-
- Mensagens: 23
- Registrado em: Dom Jun 19, 2011 13:35
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Metalúrgica e de Materiais
- Andamento: cursando
Voltar para Geometria Plana
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Equação da Circunferência
por Cleyson007 » Qui Abr 08, 2010 15:35
- 1 Respostas
- 11149 Exibições
- Última mensagem por davi_11

Dom Abr 11, 2010 13:46
Geometria Analítica
-
- Equação da circunferência
por PedroSantos » Dom Jan 09, 2011 16:38
- 3 Respostas
- 2203 Exibições
- Última mensagem por Guill

Sáb Fev 25, 2012 12:18
Geometria Plana
-
- Equação da circunferência
por Andreza » Sáb Fev 25, 2012 09:43
- 1 Respostas
- 1508 Exibições
- Última mensagem por Guill

Sáb Fev 25, 2012 11:43
Geometria Analítica
-
- Equação na Circunferência
por Fernandobertolaccini » Dom Mai 11, 2014 14:48
- 1 Respostas
- 1244 Exibições
- Última mensagem por jcmatematica

Sex Set 26, 2014 10:26
Geometria Analítica
-
- Equação da circunferencia
por brunoguim05 » Qua Mai 28, 2014 15:20
- 1 Respostas
- 1282 Exibições
- Última mensagem por jcmatematica

Sex Set 26, 2014 10:15
Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 e de
e de 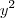 devem existir e devem ser iguais; não pode existir coeficiente para
devem existir e devem ser iguais; não pode existir coeficiente para 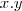 e
e 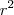 deve ser maior que 0. Na equação
deve ser maior que 0. Na equação  eu achei o
eu achei o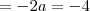 e coeficiente de
e coeficiente de 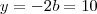 ) mas não sei como achar o raio.
) mas não sei como achar o raio.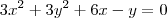 não tem nem termo independente, como se acha o raio disso?
não tem nem termo independente, como se acha o raio disso?








