por henriquefreitas » Qui Abr 28, 2011 20:12
1- Um triangulo tem lados 6,7 é numero natural O numero maximo de elementos do conjunto que podem ocupar o lugar de c é:
2- Num triangulo BAC o angulo mede 70º o angulo agudo formado pelas bissetrizes externas do angulos B e C medem em graus
Ae nesse link tem mais questao começa 10 a 16
http://www.singularsantoandre.com.br/po ... /lista.pdf POr favor me ajuda ae nao consigo fazer.
-
henriquefreitas
- Usuário Ativo
-
- Mensagens: 13
- Registrado em: Dom Abr 24, 2011 06:17
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
por Fabricio dalla » Sex Abr 29, 2011 00:42
vo responde a 1 so por enquanto
vc tem q fazer por condiçao de existencia de triangulos
7-6<c<7+6 como se trata de numeros naturais temos 11 numeros que c pode assumir respeitando a condiçao de existencia
-
Fabricio dalla
- Colaborador Voluntário
-
- Mensagens: 111
- Registrado em: Sáb Fev 26, 2011 17:50
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
por FilipeCaceres » Sex Abr 29, 2011 00:53
Você passou quase toda a sua lista para resolvê-la.
Vou fazer assim, vou postar os gabaritos que encontrei, dai você tente resolver, caso não consiga poste o que você fez em cada questão que dai vamos lhe mostrando os erros e as possíveis soluções.
Gabarito
2.
10.
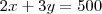
11.
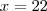
12.
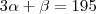
13.
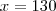
14.
15.
16.
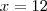
Abraço.
-
FilipeCaceres
- Colaborador Voluntário
-
- Mensagens: 351
- Registrado em: Dom Out 31, 2010 21:43
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Tec. Mecatrônica
- Andamento: formado
por henriquefreitas » Sex Abr 29, 2011 18:40
ta valeu ae
-
henriquefreitas
- Usuário Ativo
-
- Mensagens: 13
- Registrado em: Dom Abr 24, 2011 06:17
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Geometria Plana
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 10:38
Olá ! Tenho essa dúvida e não consigo montar o problema para resolução:
Qual é o racional não nulo cujo o quadrado é igual à sua terça parte ?
Grata.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 12:27
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 12:55
também pensei que fosse assim, mas a resposta é
.
Obrigada Fantini.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 13:01
Como
:
O que você fez?
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 16:17
eu só consegui fazer a igualdade, não consegui desenvolver o restante, não pensei em fatoração, mas agora entendi o que vc fez.
Obrigada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
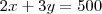
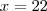
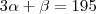
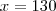
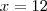
