 por stanley tiago » Dom Jan 23, 2011 18:07
por stanley tiago » Dom Jan 23, 2011 18:07
calcule x e y , sabendo que o diâmetro AB mede 12cm e MC

MB
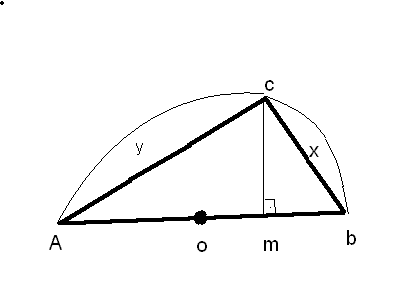
- imagem.GIF (2.84 KiB) Exibido 2292 vezes
esse foi o unico dos exercicios que eu nao consegui fazer.
agradeço a ajuda de vcs obrigado
-
stanley tiago
- Usuário Parceiro

-
- Mensagens: 57
- Registrado em: Seg Jan 17, 2011 14:23
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por DanielRJ » Dom Jan 23, 2011 20:52
por DanielRJ » Dom Jan 23, 2011 20:52
stanley tiago escreveu:calcule x e y , sabendo que o diâmetro AB mede 12cm e MC

MB
imagem.GIF
esse foi o unico dos exercicios que eu nao consegui fazer.
agradeço a ajuda de vcs obrigado
Bom não sou muito bom nesta materia mas vou tentar ajudar e com certeza alguem irá tambem ajudar vamos lá.
Primeiramente quando o lado de um triangulo é o dianmetro esse triangulo é retangulo no caso ele é retangulo em C, e logo podemos usar as relaçoes metricas.
Bom pelo o que eu entendi do enunciado o lado MC = MB Então:
MC= h
MB= h
relações metricas



Triangulo ABC logo:
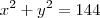

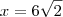
-

DanielRJ
- Colaborador Voluntário

-
- Mensagens: 254
- Registrado em: Sex Ago 20, 2010 18:19
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por stanley tiago » Dom Jan 23, 2011 22:06
por stanley tiago » Dom Jan 23, 2011 22:06
Bao noite Daniel obrigado pela a ajuda .
realmente o valor de x esta correto , porém como x = y , o y terá o mesmo valor de x .
entretanto no gabarito consta como y =
![3 \sqrt[]{2} 3 \sqrt[]{2}](/latexrender/pictures/458822d96a0bb6bc1d12a45341e1d103.png)
.
será q haveria outra maneira de vc me explicar esse exercicio?
-
stanley tiago
- Usuário Parceiro

-
- Mensagens: 57
- Registrado em: Seg Jan 17, 2011 14:23
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Geometria Plana
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Relações métricas num triângulo retângulo
por Marcampucio » Dom Abr 26, 2009 20:21
- 2 Respostas
- 7752 Exibições
- Última mensagem por Marcampucio

Ter Jun 02, 2009 13:41
Tópicos sem Interação (leia as regras)
-
- [Relações métricas no triângulo Retângulo]
 por Gustavo Gomes » Sex Out 26, 2012 21:47
por Gustavo Gomes » Sex Out 26, 2012 21:47
- 1 Respostas
- 2234 Exibições
- Última mensagem por young_jedi

Sex Out 26, 2012 22:08
Geometria Plana
-
- Relações métricas no triângulo retângulo
 por Pandaludo » Qua Ago 07, 2013 21:32
por Pandaludo » Qua Ago 07, 2013 21:32
- 0 Respostas
- 1061 Exibições
- Última mensagem por Pandaludo

Qua Ago 07, 2013 21:32
Geometria Plana
-
- Relações métricas do triângulo , tangente à uma circunferênc
por c_zaidan » Sex Out 22, 2010 15:57
- 2 Respostas
- 2206 Exibições
- Última mensagem por c_zaidan

Sex Out 22, 2010 18:50
Geometria Plana
-
- DUVIDA URGENTE : : : RELAÇOES METRICAS no Triangulo Retangul
por Mr Bob Wilson » Qua Mai 05, 2010 20:23
- 3 Respostas
- 3470 Exibições
- Última mensagem por Molina

Qua Mai 05, 2010 23:32
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 MB
MB
 MB
MB
MB



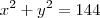

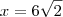

![3 \sqrt[]{2} 3 \sqrt[]{2}](/latexrender/pictures/458822d96a0bb6bc1d12a45341e1d103.png) .
.


 substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.