Estou com alguns exercícos de matemática para resolvê-los, e gostaria de saber se o que se segue está correto.
**As cidades de Quito e Cingapura encontram-se próximas
ao equador e em pontos diametralmente opostos
no globo terrestre. Considerando o raio da Terra igual
a 6 370 km, pode-se afirmar que um avião saindo de
Quito, voando em média a 800 km/h, descontando
as paradas de escalas, chega a Cingapura em aproximadamente:
a) a) 16 horas. c) 25 horas. e) 36 horas.
b) 20 horas. d) 32 horas.
Bom... eu resolvi do seguinte modo: ****Tomando como base que o globo terrestre é uma circunferência, e que me deram o valor do raio dessa circunferência, procurei encontra o diâmetro da mesma, pela fórmula :
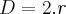 . No meu modo de pensar o diâmetro e a distância são a mesma coisa, então encontrando o comprimento, joguei na seguinte fórmula, para achar o tempo que se pede:
. No meu modo de pensar o diâmetro e a distância são a mesma coisa, então encontrando o comprimento, joguei na seguinte fórmula, para achar o tempo que se pede:  .
.Da 1ª fórmula encontrei o valor de D= 13740.
Jogando na 2ª encontrei o valor de 15,925 horas.
Como o enunciado fala que o resultado é "aproximadamente", marquei a letra a como correta.
Está correto o raciocínio?
Tenha um ótima noite.
Que Deus lhe abençoe.



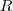 é
é 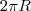 .
. que aparece na conta.
que aparece na conta.
 e
e 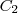 . E não o
. E não o 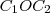 .
.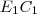 é a mesma do
é a mesma do 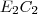 , onde
, onde 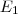 ,
,  são pontos do equador.
são pontos do equador.


 , avisa que eu resolvo.
, avisa que eu resolvo.

