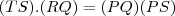por Balanar » Dom Out 17, 2010 00:47
por Balanar » Dom Out 17, 2010 00:47
Na figura ao lado,

é perpendicular a
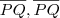
é perpendicular a <img src="http é perpendicular a


.
Prove que :
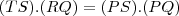
-
Balanar
- Usuário Parceiro

-
- Mensagens: 72
- Registrado em: Qua Dez 03, 2008 07:18
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Loretto » Dom Out 17, 2010 03:39
por Loretto » Dom Out 17, 2010 03:39
Nesse exercício, como trata-se de provarmos uma igualdade entre segmentos de retas, com seus respectivos ângulos adjacentes, é muito importante lembrar do seguinte teorema : " O maior lado de um triângulo é aquele oposto ao maior ângulo", e também de que " O menor lado é aquele oposto ao menor ângulo". Assim, trabalhando as incógnitas dos segmentos, chegaremos a tese procurada. Tente resolvê-lo trabalhando a partir desse teorema que você conseguirá. Um abração !!
Editado pela última vez por
Loretto em Seg Out 18, 2010 01:01, em um total de 1 vez.
-
Loretto
- Usuário Dedicado

-
- Mensagens: 28
- Registrado em: Dom Jul 25, 2010 01:35
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: exatas
- Andamento: cursando
 por VtinxD » Dom Out 17, 2010 19:52
por VtinxD » Dom Out 17, 2010 19:52
Peguemos primeiro o angulo TPS:
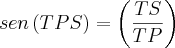
.
Como TPS e RPQ são complementares o

e

De onde tiramos a igualdade:

(1)
Como TPS e RPQ são complementares o
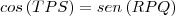
e

De onde tiramos a outra igualdade:
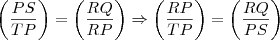
(2)
Como

e agora multiplicando em cruz a parte que nos interessa,temos:
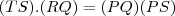
Espero ter ajudado
-
VtinxD
- Usuário Parceiro

-
- Mensagens: 64
- Registrado em: Dom Ago 15, 2010 18:29
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Bacharelado em Matematica
- Andamento: cursando
 por Balanar » Dom Out 17, 2010 21:09
por Balanar » Dom Out 17, 2010 21:09
Obrigado pela resolução VtinxD.

-
Balanar
- Usuário Parceiro

-
- Mensagens: 72
- Registrado em: Qua Dez 03, 2008 07:18
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Geometria Plana
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Demonstração envolvendo lado de triângulo
por Balanar » Ter Set 14, 2010 02:30
- 0 Respostas
- 1212 Exibições
- Última mensagem por Balanar

Ter Set 14, 2010 02:30
Geometria Plana
-
- Demonstração envolvendo ângulo
por Balanar » Qua Set 01, 2010 22:30
- 0 Respostas
- 1571 Exibições
- Última mensagem por Balanar

Qua Set 01, 2010 22:30
Geometria Plana
-
- Demonstração envolvendo bissetrizes
por Balanar » Qui Set 02, 2010 00:15
- 0 Respostas
- 1300 Exibições
- Última mensagem por Balanar

Qui Set 02, 2010 00:15
Geometria Plana
-
- Demonstração envolvendo vetores
por VFernandes » Seg Mar 07, 2011 00:59
- 0 Respostas
- 2223 Exibições
- Última mensagem por VFernandes

Seg Mar 07, 2011 00:59
Geometria Plana
-
- Demonstração envolvendo velocidade
por Cleyson007 » Sex Jul 20, 2012 10:18
- 2 Respostas
- 1574 Exibições
- Última mensagem por Russman

Sex Jul 20, 2012 11:26
Física
Usuários navegando neste fórum: Nenhum usuário registrado e 8 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 é perpendicular a
é perpendicular a 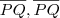 é perpendicular a <img src="http é perpendicular a
é perpendicular a <img src="http é perpendicular a 
 .
.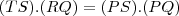

 é perpendicular a
é perpendicular a 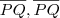 é perpendicular a <img src="http é perpendicular a
é perpendicular a <img src="http é perpendicular a 
 .
.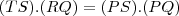


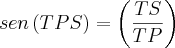 .
. e
e 
 (1)
(1)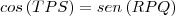 e
e 
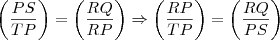 (2)
(2) e agora multiplicando em cruz a parte que nos interessa,temos:
e agora multiplicando em cruz a parte que nos interessa,temos: