 por karenblond » Qui Mar 25, 2010 17:19
por karenblond » Qui Mar 25, 2010 17:19
Uma penitenciaria tem dois patios para banhos de sol. o patio A e triangular e o B e retangular, conforme mostram as figuras, cujas dimensões estão em metros . Sabendo-se que os perimetros dos patios A e B somam 68 metros, e que Base = 1,5P pode-se afirmar que a area do patio B e igual a
A 96cm²
B 90cm²
C 84cm²
D 82cm²
E 80cm²
Por favor me ajudem.
como eu coloco essas imagens..
Editado pela última vez por
karenblond em Sex Mar 26, 2010 14:40, em um total de 1 vez.
-
karenblond
- Usuário Dedicado

-
- Mensagens: 31
- Registrado em: Qua Mar 24, 2010 14:32
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Molina » Qui Mar 25, 2010 19:47
por Molina » Qui Mar 25, 2010 19:47
karenblond escreveu:Uma penitenciaria tem dois patios para banhos de sol. o patio A e triangular e o B e retangular, conforme mostram as figuras, cujas dimensões estão em metros . Sabendo-se que os perimetros dos patios A e B somam 68 metros, e que Base = 1,5P pode-se afirmar que a area do patio B e igual a
A 96cm²
B 90cm²
C 84cm²
D 82cm²
E 80cm²
Por favor me ajudem.
Por favor, coloque a figura para alguém poder te ajudar.

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por Cleyson007 » Qui Mar 25, 2010 19:50
por Cleyson007 » Qui Mar 25, 2010 19:50
karenblond escreveu:Uma penitenciaria tem dois patios para banhos de sol. o patio A e triangular e o B e retangular, conforme mostram as figuras, cujas dimensões estão em metros . Sabendo-se que os perimetros dos patios A e B somam 68 metros, e que Base = 1,5P pode-se afirmar que a area do patio B e igual a
A 96cm²
B 90cm²
C 84cm²
D 82cm²
E 80cm²
Por favor me ajudem.
Boa noite Karen!
Karen, seria interessante você postar as figuras.. ajudaria no processo da resolução.
Sabe como colocar as imagens no fórum?
Até mais.
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por karenblond » Sex Mar 26, 2010 14:41
por karenblond » Sex Mar 26, 2010 14:41
Como eu coloco essas imagens....
-
karenblond
- Usuário Dedicado

-
- Mensagens: 31
- Registrado em: Qua Mar 24, 2010 14:32
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Cleyson007 » Sex Mar 26, 2010 17:18
por Cleyson007 » Sex Mar 26, 2010 17:18
Boa tarde Karen!
Seguem os passos:
1) Você pode escanear a imagem ou montá-la no paint.
2) Salve-a num arquivo de seu computador com o formato .jpg (devido ser mais leve)
3) Entre no site:
http://imageshack.us/ Clique em Browse
Procure onde salvou a imagem / Depois clique em abrir
Clique em "Carregar Agora"
Após carregar, copie o link direto (lado esquerdo do site)
Agora já está meio caminho andado

No fórum do Ajuda Matemática, clique no botão
Img e cole o link que você copiou.
Para evitar erros, clique no botão prever antes de enviar, ok?
Comente qualquer dúvida

Até mais.
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por karenblond » Seg Mar 29, 2010 18:13
por karenblond » Seg Mar 29, 2010 18:13

Vamos ver se da para me ajudarem.
-
karenblond
- Usuário Dedicado

-
- Mensagens: 31
- Registrado em: Qua Mar 24, 2010 14:32
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Molina » Ter Mar 30, 2010 00:35
por Molina » Ter Mar 30, 2010 00:35
Boa noite, Karen.
Vamos primeiramente usar a informação que a soma dos perímetros do retângulo e do triângulo é 68:

O perímetro do triângulo é dado por

e o perímetro do retângulo, por

, somando os dois:


Agora usaremos a informação que
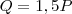
e substituiremos na fórmula a cima:
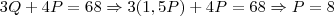
Como
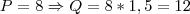
Temos então a base e a altura do retângulo que queremos descobrir a área:
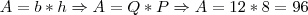
Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
Voltar para Geometria Plana
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Razão da área do triângulo para a área do quadrilátero]
 por Mayra Luna » Sex Nov 23, 2012 20:17
por Mayra Luna » Sex Nov 23, 2012 20:17
- 2 Respostas
- 4416 Exibições
- Última mensagem por Mayra Luna

Ter Nov 27, 2012 14:53
Geometria Plana
-
- Área - Na próxima figura ABCD é um quadrilátero de área 200
 por marguiene » Sex Out 10, 2014 10:22
por marguiene » Sex Out 10, 2014 10:22
- 0 Respostas
- 2130 Exibições
- Última mensagem por marguiene

Sex Out 10, 2014 10:22
Geometria Plana
-
- Área - Na figura abaixo ABCD é um retângulo de área 11 cm².
 por marguiene » Sex Out 10, 2014 10:35
por marguiene » Sex Out 10, 2014 10:35
- 0 Respostas
- 2901 Exibições
- Última mensagem por marguiene

Sex Out 10, 2014 10:35
Geometria Plana
-
- [Área] Área de triangulo e trapézio
 por smlspirit » Qui Jul 19, 2012 20:07
por smlspirit » Qui Jul 19, 2012 20:07
- 1 Respostas
- 2996 Exibições
- Última mensagem por e8group

Qui Jul 19, 2012 20:57
Geometria Plana
-
- Área
 por flavio2010 » Sex Jul 23, 2010 19:21
por flavio2010 » Sex Jul 23, 2010 19:21
- 1 Respostas
- 1330 Exibições
- Última mensagem por Lucio Carvalho

Sex Jul 23, 2010 20:12
Números Complexos
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
zig - Sex Set 23, 2011 13:57
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
Vennom - Sex Set 23, 2011 21:41
zig escreveu:![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Rpz, o negócio é o seguinte:
Quando você tem uma potência negativa, tu deve inverter a base dela. Por exemplo:

Então pense o seguinte: a fração geratriz de 0,05 é

, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
Veja:
![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
A raiz quadrada de vinte, você acha fácil, né?
Espero ter ajudado.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:23
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:24
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.









 e o perímetro do retângulo, por
e o perímetro do retângulo, por  , somando os dois:
, somando os dois:

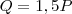 e substituiremos na fórmula a cima:
e substituiremos na fórmula a cima: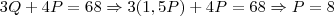
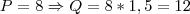
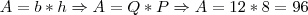
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.