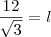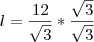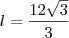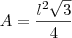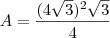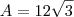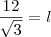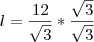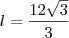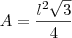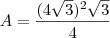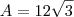por luquinhass12 » Seg Dez 03, 2012 16:59
por luquinhass12 » Seg Dez 03, 2012 16:59
- Anexos
-

Editado pela última vez por
luquinhass12 em Qua Dez 05, 2012 02:35, em um total de 1 vez.
-
luquinhass12
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Seg Dez 03, 2012 16:54
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por MarceloFantini » Seg Dez 03, 2012 19:48
por MarceloFantini » Seg Dez 03, 2012 19:48
Luquinhas, bem vindo ao fórum. Por favor, digite todo o enunciado do exercício juntamente com sua tentativa de resolução. Para tanto, utilize LaTEX, uma linguagem que facilita a escrita de fórmulas. Existem tutoriais no fórum.
Seu tópico não deverá ser respondido até estar de acordo com as regras.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por luquinhass12 » Qua Dez 05, 2012 02:35
por luquinhass12 » Qua Dez 05, 2012 02:35
Pronto demorei um pouco, mas ta ai

desculpa qualquer coisa e obrigado.
-
luquinhass12
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Seg Dez 03, 2012 16:54
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por MarceloFantini » Qui Dez 06, 2012 00:49
por MarceloFantini » Qui Dez 06, 2012 00:49
Suas contas parecem estar corretas, de acordo com as definições. O gabarito não bate ou você queria ter certeza?
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por luquinhass12 » Sex Dez 07, 2012 00:41
por luquinhass12 » Sex Dez 07, 2012 00:41
Não tem essa alternativa no gabarito, como mostra na imagem ;s
-
luquinhass12
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Seg Dez 03, 2012 16:54
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por MarceloFantini » Sex Dez 07, 2012 02:11
por MarceloFantini » Sex Dez 07, 2012 02:11
Fiz as contas e foram exatamente iguais. A questão deve estar errada. Você tem a resposta?
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por luquinhass12 » Sáb Dez 08, 2012 01:07
por luquinhass12 » Sáb Dez 08, 2012 01:07
resposta é letra a)
mas está errada mesmo, e não foi anulado pois não entraram com recurso que é depois de 48h da prova e tem que entregar manuscrito e na sede da universidade que é em outra cidade (não é na capital).
Mas obrigado pelas respostas

-
luquinhass12
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Seg Dez 03, 2012 16:54
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Geometria Plana
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Geometria - plano e curva
por marinalcd » Seg Ago 20, 2012 21:04
- 1 Respostas
- 1436 Exibições
- Última mensagem por Russman

Ter Ago 21, 2012 02:52
Geometria Analítica
-
- Geometria Analítica no plano
por Ana Margarida » Dom Dez 27, 2015 18:15
- 2 Respostas
- 3650 Exibições
- Última mensagem por Ana Margarida

Dom Dez 27, 2015 21:12
Geometria Plana
-
- Geometria Analítica no plano
por Ana Margarida » Dom Dez 27, 2015 22:05
- 5 Respostas
- 6130 Exibições
- Última mensagem por Ana Margarida

Seg Dez 28, 2015 23:59
Geometria Analítica
-
- Geometria Analítica no plano
por Ana Margarida » Ter Dez 29, 2015 15:07
- 1 Respostas
- 3627 Exibições
- Última mensagem por DanielFerreira

Dom Fev 07, 2016 20:51
Geometria Plana
-
- [GEOMETRIA ANALÍTICA - PLANO CARTESIANO]
 por maiconaguiar » Ter Dez 02, 2014 13:23
por maiconaguiar » Ter Dez 02, 2014 13:23
- 1 Respostas
- 2245 Exibições
- Última mensagem por Cleyson007

Ter Dez 02, 2014 15:01
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.