CUBO

por **Thassya** » Seg Out 11, 2010 21:46

Por favor me ajudem com essa questão!!!
URGENTEEEEEEEEEEEEEEE

Uma fatia de 3cm de espessura é cortada de um cubo, deixando um volume de 108cm CUBICOS . Encontre o
comprimento do lado do cubo original

por **MarceloFantini** » Ter Out 12, 2010 04:21

Vamos chamar o lado do novo cubo de

. Então

, e o lado do volume antigo será a+3

. $a = \sqrt[3]{108} = 3 \sqrt[3]{2^2}$ e o lado $a+3 = 3 \sqrt[3]{2^2} + 3 = 3(1 + \sqrt[3]{2^2})$

por **Augusto Evaristo** » Sáb Out 16, 2010 01:33

Fantini escreveu:Vamos chamar o lado do novo cubo de . Então , e o lado do volume antigo será . $a = \sqrt[3]{108} = 3 \sqrt[3]{2^2}$ e o lado $a+3 = 3 \sqrt[3]{2^2} + 3 = 3(1 + \sqrt[3]{2^2})$

Cara Thassya e Caro Fantini,

É um prazer trazer a minha participação para essa questão.

Tenho a corrigir humildemente um tetalhe, e peço desde já sua permissão.

Quando a questão chama a figura geométrica de cubo, implica em dizer que ela tem as arestas iguais e seu volume será dado pela seguinte fórmula:

$V={a}^{3}$

No entanto, a questão diz que desse cubo é retirada uma fatia, observemos bem, uma fatia e tão somente uma fatia, que significa seccionar o cubo, e no tamanho de 3 cm de espessura, o que implica dizer que interfere em apenas uma das medidas da figura que passará a se chamar paralelepípedo. Corrijam-me se eu estiver errado. Logo a medida do seu volume será dada pelo produto da base com a altura e a profundidade será dada agora pela seguinte fórmula:

V=a.a.(a-3)

$V={a}^{2}.(a-3)$
$V={a}^{3}-3a$
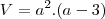
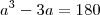
${a}^{3}-3a=180$
${a}^{3}-3a-180=0$

Agora deixo para você desenvolver essa equação cúbica por Cardano.

Foi um prazer ajudar.

por **Elcioschin** » Sáb Out 16, 2010 18:50

O Augusto está com razão, com duas ressalvas:
O correto é 108 e não é 180.
Não é necessário Cardano:

a³ - 3a² - 108 = 0 ----> 108 = 2²*3³ ----> Divisores de 108: + - 1, 2, 3, 4, 6,12, 27, 36, 54, 108,

(a - 3)*a² = 108 ----> (a - 3)*a² = 3*36 ----> (a - 3)*a² = 3*6² ----> a = 6

por **Augusto Evaristo** » Dom Out 17, 2010 16:06

Elcioschin escreveu:O Augusto está com razão, com duas ressalvas:
O correto é 108 e não é 180.
Não é necessário Cardano:

a³ - 3a² - 108 = 0 ----> 108 = 2²*3³ ----> Divisores de 108: + - 1, 2, 3, 4, 6,12, 27, 36, 54, 108,

(a - 3)*a² = 108 ----> (a - 3)*a² = 3*36 ----> (a - 3)*a² = 3*6² ----> a = 6

Olá Elciochin,

Agradeço pelas suas ressalvas. É esse o espírito desse forum.

Parabéns!

por **MarceloFantini** » Dom Out 17, 2010 16:14

E eu o agradeço por ter consertado a resolução. Obrigado.

por **Caroline Maul** » Qua Out 20, 2010 21:20

Elcioschin escreveu:O Augusto está com razão, com duas ressalvas:
O correto é 108 e não é 180.
Não é necessário Cardano:

a³ - 3a² - 108 = 0 ----> 108 = 2²*3³ ----> Divisores de 108: + - 1, 2, 3, 4, 6,12, 27, 36, 54, 108,

(a - 3)*a² = 108 ----> (a - 3)*a² = 3*36 ----> (a - 3)*a² = 3*6² ----> a = 6

Perdoe minha ignorância, mas no final o que vc fez... pegou os termos elevados ao mesmo expoente e igualou???
Assim: a-3=3 -> a=6 ou a²=6²->a=6?? Caso foi isso, esse método pode sempre ser usado em multiplicações no estilo dessa??
O negócio dos divisores foi só pra encontrar valores que pudessem ser usados dessa forma??

Desde já agradeço a resposta!!