 por JoseEduardo » Dom Set 26, 2010 02:29
por JoseEduardo » Dom Set 26, 2010 02:29
Vi este desafio recentemente e ainda não encontrei solução:
Desenhei um quadrado com 60 unidades de lado e dentro dele desenhei 4 círculos iguais. Quais as suas áreas?
Agradeceria muito uma explicação sobre como resolve-lo.
-
JoseEduardo
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Sex Set 10, 2010 01:45
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Estudante
- Andamento: cursando
 por MarceloFantini » Dom Set 26, 2010 02:43
por MarceloFantini » Dom Set 26, 2010 02:43
Talvez fique difícil entender sem figura, mas: para que os 4 círculos sejam iguais, eles devem ser tangentes entre si e ao quadrado e tenham raios iguais. Se você unir os raios em uma linha reta, verá que:

. Logo:
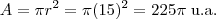
.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por JoseEduardo » Dom Set 26, 2010 15:36
por JoseEduardo » Dom Set 26, 2010 15:36
Muito obrigado pela ajuda, agora percebi como fica simples, também percebi que pode se encontrar o raio desse jeito: 2 diametros = 60, logo 1 diametro = 30, e um raio = 15!
valeu

-
JoseEduardo
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Sex Set 10, 2010 01:45
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Estudante
- Andamento: cursando
Voltar para Geometria Plana
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Problema de geometria !
 por LuizCarlos » Qui Ago 25, 2011 17:23
por LuizCarlos » Qui Ago 25, 2011 17:23
- 3 Respostas
- 1788 Exibições
- Última mensagem por LuizCarlos

Sex Ago 26, 2011 15:35
Geometria Plana
-
- geometria problema com incentro
por correiomar » Seg Set 07, 2009 23:08
- 6 Respostas
- 12568 Exibições
- Última mensagem por juuheuh

Sáb Mai 21, 2016 13:11
Geometria Plana
-
- Problema envolvendo geometria
por Carlos28 » Sex Mai 09, 2014 21:46
- 1 Respostas
- 1379 Exibições
- Última mensagem por young_jedi

Sex Mai 09, 2014 22:15
Geometria Plana
-
- Problema envolvendo geometria e area!
 por bmachado » Seg Mar 05, 2012 22:55
por bmachado » Seg Mar 05, 2012 22:55
- 4 Respostas
- 4138 Exibições
- Última mensagem por bmachado

Seg Mar 05, 2012 23:48
Geometria Plana
-
- Problema de Geometria com resposta em porcentagem
por Macedo Junior » Sex Jul 22, 2016 12:20
- 2 Respostas
- 9208 Exibições
- Última mensagem por Macedo Junior

Sex Jul 22, 2016 16:08
Geometria Plana
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



 . Logo:
. Logo: 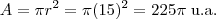 .
.


