 por Anderson POntes » Sex Jul 09, 2010 01:24
por Anderson POntes » Sex Jul 09, 2010 01:24

- Figura da questao!!!
- imagem.GIF (4.97 KiB) Exibido 4332 vezes
No modelo acima, estão representadas três caixas iguais
(paralelepípedos reto-retângulos), de dimensões a, a e h.
Se o conjunto ocupa 162 cm3, qual é, em cm2, a área total
de cada caixa?
(A) 54
(B) 72
(C) 90
(D) 108
(E) 144
Respondi;
Volume:
V=largura.comprimento.altura
V=162cm³
V/3=54cm³
na figura;
h=2.a
e o resto existe alguma relação enter volume e area?
Agradeço..
-
Anderson POntes
- Usuário Ativo

-
- Mensagens: 24
- Registrado em: Qui Jul 08, 2010 17:53
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: tecnico eletrotécnica
- Andamento: formado
 por Tom » Sex Jul 09, 2010 01:44
por Tom » Sex Jul 09, 2010 01:44
Sabemos que o volume do paralelepípedo é dado pelo produto das dimensões, isto é,
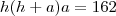
, mas como
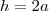
(Basta observar a simetria da figura),temos:
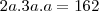
, isto é,

e assim

cm, logo

cm
Desejamos obter a área total de cada caixa, isto é, a soma da área de cada uma de suas faces laterais. Assim:

Tom
-
Tom
- Usuário Parceiro

-
- Mensagens: 75
- Registrado em: Sex Jul 02, 2010 00:42
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Automação e Controle Industrial
- Andamento: formado
 por Anderson POntes » Sex Jul 09, 2010 01:59
por Anderson POntes » Sex Jul 09, 2010 01:59
Muito obrigado pela belissima explicação companheiro..
-
Anderson POntes
- Usuário Ativo

-
- Mensagens: 24
- Registrado em: Qui Jul 08, 2010 17:53
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: tecnico eletrotécnica
- Andamento: formado
Voltar para Geometria Plana
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Ajuda aqui com essa questão de função
por Ronaldobb » Qui Set 20, 2012 19:41
- 7 Respostas
- 3353 Exibições
- Última mensagem por Ronaldobb

Qui Set 20, 2012 22:34
Funções
-
- Preciso de ajuda com essa questão da Fundação Cesgranrio
por Jesicaa » Qui Mar 12, 2015 11:46
- 2 Respostas
- 3141 Exibições
- Última mensagem por Jesicaa

Dom Mar 15, 2015 00:06
Sistemas de Equações
-
- Vólume e área
por pedroph123 » Sex Jul 15, 2011 14:30
- 1 Respostas
- 1437 Exibições
- Última mensagem por LuizAquino

Sex Jul 15, 2011 16:31
Cálculo: Limites, Derivadas e Integrais
-
- calculo area e volume - integral
por bicio29 » Qui Out 20, 2011 08:41
- 3 Respostas
- 4040 Exibições
- Última mensagem por LuizAquino

Qui Out 20, 2011 10:30
Cálculo: Limites, Derivadas e Integrais
-
- Aplicaçãoes da integral- Area e volume
por Erick » Dom Jun 09, 2013 15:15
- 1 Respostas
- 2339 Exibições
- Última mensagem por KathleenH

Qui Jun 27, 2013 16:35
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



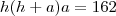 , mas como
, mas como 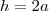 (Basta observar a simetria da figura),temos:
(Basta observar a simetria da figura),temos: 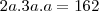 , isto é,
, isto é,  e assim
e assim  cm, logo
cm, logo  cm
cm


 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
