 por Thainara » Qui Mai 19, 2016 12:08
por Thainara » Qui Mai 19, 2016 12:08
As diagonais de um losango estão entre si na razão 1:3.Se o lado desse losango mede 5cm, a sua área, em centímetros quadrados é:
a)15 d)25\sqrt[]{10}
b)25 e)30\sqrt[]{10}
c)30
Eu sei que para calcular a área de um losango basta eu multiplicar duas diagonais e dividir por 2,mas como encontro o valor das diagonais?
-
Thainara
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Ter Mai 17, 2016 23:50
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Daniel Bosi » Qui Mai 19, 2016 14:13
por Daniel Bosi » Qui Mai 19, 2016 14:13
Olá Thainara,
Primeiro devemos perceber que as diagonais do losango estão entre si na razão 1:3, o que significa que a diagonal maior é o triplo da menor:

Se sabemos que o lado do losango mede 5, podemos pensar que o lado do losango é uma hipotenusa cujos catetos são as metades das diagonais. Usando o Teorema de Pitágoras:
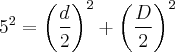
Como sabemos que

:
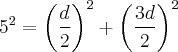
Se você resolver essa equação vai encontrar o valor de
![d=\sqrt[]{10} d=\sqrt[]{10}](/latexrender/pictures/bdc6256e2fe6dfea220a4abee29f6531.png)
, que é a diagonal menor. A diagonal maior é

, portanto basta multiplicar o valor de

por 3 e encontrar
![D=3\times\sqrt[]{10} D=3\times\sqrt[]{10}](/latexrender/pictures/020d6658192a05ce57cd2137b2be9ffe.png)
.
O resultado final da área do losango deve ser 15.
-
Daniel Bosi
- Usuário Dedicado

-
- Mensagens: 26
- Registrado em: Seg Mai 16, 2016 21:37
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por Thainara » Qui Mai 19, 2016 15:27
por Thainara » Qui Mai 19, 2016 15:27
Muito obrigada Daniel!Agora eu consegui resolver a questão!
-
Thainara
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Ter Mai 17, 2016 23:50
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
Voltar para Geometria Plana
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Dúvidas em Pa, alguém poderia me ajudar?
por plugpc » Qui Out 01, 2009 18:22
- 2 Respostas
- 1905 Exibições
- Última mensagem por DanielFerreira

Sex Out 02, 2009 01:08
Álgebra Elementar
-
- Alguem poderia me ajudar com esse exercicio ?
por rodrigo321 » Dom Dez 06, 2009 03:33
- 1 Respostas
- 2011 Exibições
- Última mensagem por Molina

Dom Dez 06, 2009 12:09
Cálculo: Limites, Derivadas e Integrais
-
- Alguem poderia me ajudar nesse exercicio?
por davi1993 » Seg Jun 20, 2011 12:51
- 4 Respostas
- 2470 Exibições
- Última mensagem por davi1993

Seg Jun 20, 2011 15:52
Funções
-
- Alguém poderia me ajudar a responder esses exercícios.?
por icarowilliams15 » Seg Jun 13, 2011 12:12
- 7 Respostas
- 4319 Exibições
- Última mensagem por icarowilliams15

Qua Jun 15, 2011 10:57
Funções
-
- [geometria analitica-vetores]alguém poderia resolver?
por amanda_k » Sáb Out 14, 2017 22:28
- 0 Respostas
- 4044 Exibições
- Última mensagem por amanda_k

Sáb Out 14, 2017 22:28
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



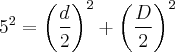
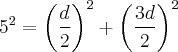
![d=\sqrt[]{10} d=\sqrt[]{10}](/latexrender/pictures/bdc6256e2fe6dfea220a4abee29f6531.png) , que é a diagonal menor. A diagonal maior é
, que é a diagonal menor. A diagonal maior é  por 3 e encontrar
por 3 e encontrar ![D=3\times\sqrt[]{10} D=3\times\sqrt[]{10}](/latexrender/pictures/020d6658192a05ce57cd2137b2be9ffe.png) .
.
 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
