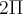* rad
vale 3,14 e 180º. Eis a dúvida de conversão. Quando o rad vier multiplicado por último na expressão ( 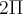* rad ) , o valor será de 3,14 ? Quando não houver rad, o valor virá em graus ?Eu vi uma demonstração do valor do rad, mas não entendi claramente. Eles circunscreveram um hexágono. A razão entre uma "corda", que é ligada a dois vértices do hexágono, e o raio do círculo era igual a 1 rad.
Mas tá meio misturado na minha cabeça, e eu queria entender melhor as relações, para não esquecer "essas misturas de informação" daqui alguns dias.
Grato.
nada mais é do que o número de vezes que o raio cabe em um arco de circunferência de 180°. É como se pegássemos o raio e o 'escorregássemos' no arco. Ele caberia 3 vezes e mais um pouquinho, que é o que vem depois da vírgula. Por isso o nome 'radiano'.![{[0,2\pi]}](/latexrender/pictures/a283116befea00f0ab60c7b5415b65b4.png "{[0,2\pi]}")
está em radianos. Ele pode dizer também ![{[0,6]}](/latexrender/pictures/e3c148ca53667ea09ae89049adee3025.png "{[0,6]}")
. Quando vier em graus ele te dirá. Em geral, eles não misturam graus com radianos. No segundo exemplo, note que não é uma volta completa (360°), pois então seria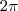 
(aproximadamente 6,28).
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
o ângulo entre o eixo horizontal e o afixo 
. O triângulo é retângulo com catetos 
e 
, tal que 
. Seja 
o ângulo complementar. Então 
. Como 
, o ângulo que o afixo 
formará com a horizontal será 
, então 
. Como módulo é um: 
.
.