 por Thais Camerino » Seg Jul 07, 2014 15:22
por Thais Camerino » Seg Jul 07, 2014 15:22
Olá gente! Não sei como resolver este tipo de problema assim proposto.. Gostaria de pedir para alguem ajudar-me a entender este tipo de exercicio..
O raio do circulo
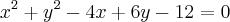
é :
Agradecida!
-
Thais Camerino
- Usuário Ativo

-
- Mensagens: 14
- Registrado em: Dom Abr 27, 2014 00:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Design
- Andamento: cursando
 por e8group » Seg Jul 07, 2014 22:44
por e8group » Seg Jul 07, 2014 22:44
Dica : Completar quadrados para poder escrever a eq. sob a forma
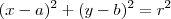
.
Exemplo :
![x^2 -2x = [x^2 - 2x +1] - 1 = [x-1]^2 - 1 x^2 -2x = [x^2 - 2x +1] - 1 = [x-1]^2 - 1](/latexrender/pictures/e647ba3a6877a57b6bbd256659d01186.png)
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Thais Camerino » Ter Jul 08, 2014 02:45
por Thais Camerino » Ter Jul 08, 2014 02:45
Quando eu fiz, deu x = 2 e y = -3
Depois calculo do raio : R =
![\sqrt[]{2^2 + \left(-3 \right)^2 - 12} \sqrt[]{2^2 + \left(-3 \right)^2 - 12}](/latexrender/pictures/0e19e8f5735a2fa5c6d2438498048e3f.png)
No que deu 1.. mas o resultado final é 5 :s
-
Thais Camerino
- Usuário Ativo

-
- Mensagens: 14
- Registrado em: Dom Abr 27, 2014 00:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Design
- Andamento: cursando
 por Thais Camerino » Ter Jul 08, 2014 02:54
por Thais Camerino » Ter Jul 08, 2014 02:54
Ah, já vi o meu erro. Muito obrigada pela tua Santhiago !!
-
Thais Camerino
- Usuário Ativo

-
- Mensagens: 14
- Registrado em: Dom Abr 27, 2014 00:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Design
- Andamento: cursando
Voltar para Geometria Plana
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- porcentagem com o raio do circulo
por hevhoram » Ter Mai 31, 2011 12:15
- 2 Respostas
- 5048 Exibições
- Última mensagem por hevhoram

Qui Jun 02, 2011 16:11
Álgebra Elementar
-
- Determine a medida aproximada do raio do circulo
por andersontricordiano » Qui Abr 14, 2011 20:00
- 1 Respostas
- 4198 Exibições
- Última mensagem por FilipeCaceres

Qui Abr 14, 2011 20:10
Geometria
-
- Medida do raio do círculo inscrito no trapézio retângulo
 por gustavoluiss » Seg Dez 13, 2010 08:33
por gustavoluiss » Seg Dez 13, 2010 08:33
- 5 Respostas
- 7298 Exibições
- Última mensagem por gustavoluiss

Ter Dez 28, 2010 19:21
Geometria Plana
-
- Círculo trigonométrico
 por Ananda » Sex Fev 29, 2008 10:56
por Ananda » Sex Fev 29, 2008 10:56
- 8 Respostas
- 7527 Exibições
- Última mensagem por Ananda

Seg Mar 03, 2008 17:51
Trigonometria
-
- Círculo trigonométrico
 por Ananda » Qui Mar 06, 2008 23:00
por Ananda » Qui Mar 06, 2008 23:00
- 1 Respostas
- 3702 Exibições
- Última mensagem por Neperiano

Dom Set 04, 2011 22:07
Geometria
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
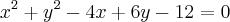 é :
é : 
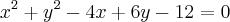 é :
é : 
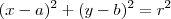 .
. ![x^2 -2x = [x^2 - 2x +1] - 1 = [x-1]^2 - 1 x^2 -2x = [x^2 - 2x +1] - 1 = [x-1]^2 - 1](/latexrender/pictures/e647ba3a6877a57b6bbd256659d01186.png)

![\sqrt[]{2^2 + \left(-3 \right)^2 - 12} \sqrt[]{2^2 + \left(-3 \right)^2 - 12}](/latexrender/pictures/0e19e8f5735a2fa5c6d2438498048e3f.png)


 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.