Olá
garrincha, seja bem-vindo!
Este exercício é bem interessante.
Mas, por favor, leia as regras do fórum.
Aqui é fundamental seu comentário sobre tentativas e dificuldades.
Como dica, sugiro seguir os seguintes passos:
1) Imagine "enxergar" a bicicleta de cima.
Reflita sobre a trajetória de cada roda.
Inicialmente, considere em linha reta, depois "vire o guidão" aos poucos;
2) Em seguida, pense como deveria ficar o guidão para que a roda traseira circulasse sobre um único ponto, ou seja, para que não houvesse círculo descrito pela roda traseira.
Concorda que neste nosso outro exemplo, o guidão deveria ficar alinhado com a roda traseira, em outras palavras, a roda dianteira deveria formar um ângulo de

com a roda traseira?
Pois bem, citei este caso particular apenas para facilitar a visualização de que
a roda tangencia o círculo formado pela trajetória;
3) Então, tente desenhar esta visão superior planificada (em duas dimensões).
Comece pelas rodas alinhadas representadas por dois segmentos de reta iguais, considerando a distância de 1,2m entre seus centros;
4) Desenhe novamente a roda dianteira com a inclinação de
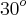
;
5) Trace uma perpendicular a cada roda, passando pelo seus respectivos centros.
Repare que a intersecção destas perpendiculares é o centro das duas trajetórias circulares;
6) Com um compasso, marque o raio maior e faça o círculo da trajetória dianteira;
7) Marque o raio menor da mesma forma e faça o círculo da trajetória traseira;
8) Una os dois pontos médios dos segmentos que representam as rodas;
9) Veja o triângulo retângulo principal obtido. Prolongue o segmento da roda dianteira inclinada e obtenha outro triângulo retângulo menor;
10) Marque todos os ângulos, considerando: o ângulo oposto pelo vértice, semelhança de triângulos e soma de ângulos internos de um triângulo;
11) Repare e anote na figura que: a hipotenusa do triângulo retângulo maior é o raio

do círculo descrito pela roda dianteira;
12) O raio

do círculo descrito pela roda traseira é o cateto adjacente ao ângulo de
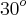
, no mesmo triângulo;
13) Calcule os raios

e

com seno e tangente, respectivamente;
Espero ter ajudado e:
14) Aguardo seus comentários.
Caso tenha a resposta, favor confirmar:

metros
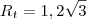
metros
Vamos conversando...



 com a roda traseira?
com a roda traseira?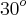 ;
; do círculo descrito pela roda dianteira;
do círculo descrito pela roda dianteira; do círculo descrito pela roda traseira é o cateto adjacente ao ângulo de
do círculo descrito pela roda traseira é o cateto adjacente ao ângulo de 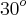 , no mesmo triângulo;
, no mesmo triângulo; e
e  com seno e tangente, respectivamente;
com seno e tangente, respectivamente; metros
metros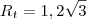 metros
metros



 e
e  possuem raio de mesma medida ("Um ciclista pedala uma bicicleta com rodas de mesmo diâmetro...").
possuem raio de mesma medida ("Um ciclista pedala uma bicicleta com rodas de mesmo diâmetro..."). ("...com distância entre os eixos de 1,20m...").
("...com distância entre os eixos de 1,20m..."). :
: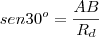
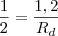
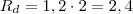 metros
metros :
: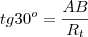

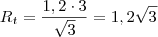 metros
metros

 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.