 por garrincha » Sex Abr 11, 2008 23:53
por garrincha » Sex Abr 11, 2008 23:53
(Unicamp-SP)Um ciclista pedala uma bicicleta com rodas de mesmo diâmetro e com distância entre os eixos de 1,20m.Num determinado instante ele vira o guidão em 30 (graus) e o mantêm nessa posição para andar em círculo.Calcule os raios dos círculos descritos pelas rodas dianteira e traseira da bicicleta.
-
garrincha
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Dom Mar 02, 2008 01:37
- Área/Curso: Estudante
- Andamento: cursando
 por admin » Sáb Abr 12, 2008 01:33
por admin » Sáb Abr 12, 2008 01:33
Olá
garrincha, seja bem-vindo!
Este exercício é bem interessante.
Mas, por favor, leia as regras do fórum.
Aqui é fundamental seu comentário sobre tentativas e dificuldades.
Como dica, sugiro seguir os seguintes passos:
1) Imagine "enxergar" a bicicleta de cima.
Reflita sobre a trajetória de cada roda.
Inicialmente, considere em linha reta, depois "vire o guidão" aos poucos;
2) Em seguida, pense como deveria ficar o guidão para que a roda traseira circulasse sobre um único ponto, ou seja, para que não houvesse círculo descrito pela roda traseira.
Concorda que neste nosso outro exemplo, o guidão deveria ficar alinhado com a roda traseira, em outras palavras, a roda dianteira deveria formar um ângulo de

com a roda traseira?
Pois bem, citei este caso particular apenas para facilitar a visualização de que
a roda tangencia o círculo formado pela trajetória;
3) Então, tente desenhar esta visão superior planificada (em duas dimensões).
Comece pelas rodas alinhadas representadas por dois segmentos de reta iguais, considerando a distância de 1,2m entre seus centros;
4) Desenhe novamente a roda dianteira com a inclinação de
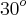
;
5) Trace uma perpendicular a cada roda, passando pelo seus respectivos centros.
Repare que a intersecção destas perpendiculares é o centro das duas trajetórias circulares;
6) Com um compasso, marque o raio maior e faça o círculo da trajetória dianteira;
7) Marque o raio menor da mesma forma e faça o círculo da trajetória traseira;
8) Una os dois pontos médios dos segmentos que representam as rodas;
9) Veja o triângulo retângulo principal obtido. Prolongue o segmento da roda dianteira inclinada e obtenha outro triângulo retângulo menor;
10) Marque todos os ângulos, considerando: o ângulo oposto pelo vértice, semelhança de triângulos e soma de ângulos internos de um triângulo;
11) Repare e anote na figura que: a hipotenusa do triângulo retângulo maior é o raio

do círculo descrito pela roda dianteira;
12) O raio

do círculo descrito pela roda traseira é o cateto adjacente ao ângulo de
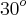
, no mesmo triângulo;
13) Calcule os raios

e

com seno e tangente, respectivamente;
Espero ter ajudado e:
14) Aguardo seus comentários.
Caso tenha a resposta, favor confirmar:

metros
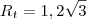
metros
Vamos conversando...
-

admin
- Colaborador Administrador - Professor

-
- Mensagens: 885
- Registrado em: Qui Jul 19, 2007 10:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática IME-USP
- Andamento: formado
 por garrincha » Sáb Abr 12, 2008 18:16
por garrincha » Sáb Abr 12, 2008 18:16
Caro Fábio,muito grato pela resposta.O problema foi de interpretação e abstração.A questão,respondida de maneira brilhante,e com uma linguagem bastante clara e precisa,está com o gabarito correto.Vejo q usou os conceitos de mediatriz (raio das circ.) para descrever a situação,bem como a semelhança de triângulos.Peço q me oriente no uso correto do fórum,pois sou péssimo em computador.Realmente estou muito grato pela sua atenção e paciência.Saudações.
-
garrincha
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Dom Mar 02, 2008 01:37
- Área/Curso: Estudante
- Andamento: cursando
 por admin » Sáb Abr 12, 2008 21:27
por admin » Sáb Abr 12, 2008 21:27
Olá!
Realmente, como você disse, as mediatrizes dos segmentos das rodas são raios das circunferências.
Na construção do desenho optei por chamá-las de perpendiculares que passam pelo centro dos segmentos.
Sobre a semelhança dos triângulos retângulos, há um teorema relacionado:
Em todo triângulo retângulo, a altura relativa à hipotenusa determina dois triângulos retângulos semelhantes ao primeiro e semelhantes entre si.
A demonstração utiliza o primeiro caso AA de semelhança de triângulos (ângulo-ângulo).
Depois, será interessante finalizarmos este tópico com uma figura.
Sobre o uso do fórum, é simples. Em resumo:
1) Juntamente com o enunciado, envie também comentários sobre suas tentativas e dificuldades, especificando as dúvidas;
2) Caso haja expressões matemáticas no exercício, utilize LaTeX na postagem, através do botão "editor de fórmulas".
Bons estudos.
Até mais!
-

admin
- Colaborador Administrador - Professor

-
- Mensagens: 885
- Registrado em: Qui Jul 19, 2007 10:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática IME-USP
- Andamento: formado
 por admin » Qua Abr 23, 2008 14:18
por admin » Qua Abr 23, 2008 14:18
Idéia inicial da visão superior:
-

admin
- Colaborador Administrador - Professor

-
- Mensagens: 885
- Registrado em: Qui Jul 19, 2007 10:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática IME-USP
- Andamento: formado
 por admin » Sex Mai 09, 2008 18:55
por admin » Sex Mai 09, 2008 18:55
Uma figura com mais detalhes:
Zoom na região mais importante:
Onde as circunferências

e
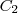
possuem raio de mesma medida ("Um ciclista pedala uma bicicleta com rodas de mesmo diâmetro...").
E

("...com distância entre os eixos de 1,20m...").
Obtendo

:
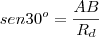
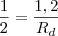
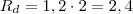
metros
Obtendo

:
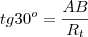

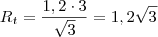
metros
-

admin
- Colaborador Administrador - Professor

-
- Mensagens: 885
- Registrado em: Qui Jul 19, 2007 10:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática IME-USP
- Andamento: formado
 por Mi_chelle » Seg Mar 28, 2011 17:55
por Mi_chelle » Seg Mar 28, 2011 17:55
Olá,
Fiz questão de me registrar, para agradecer a ajuda!!
Ao ler o enunciado em minha apostila, achei que nunca iria resolver a questão. Quando pesquisei na internet, achei aqui a solução para o problema.
A resolução matemática é simples, a chave é a visualização do trajeto das rodas.
E com os ótimos comentário e desenho, feito de maneira simples, consegui resolver rapidamente a questão.
Obrigada mais uma vez,
Mi.
-
Mi_chelle
- Usuário Ativo

-
- Mensagens: 21
- Registrado em: Seg Mar 28, 2011 17:35
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Tec. Química
- Andamento: formado
Voltar para Geometria Plana
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Continuidade - Dúvida questão, é urgente!!
por arthurvct » Seg Mai 06, 2013 18:37
- 1 Respostas
- 1097 Exibições
- Última mensagem por e8group

Seg Mai 06, 2013 22:11
Cálculo: Limites, Derivadas e Integrais
-
- Dúvida Urgente - Questão difícil
 por marcelojs » Ter Jun 11, 2013 23:43
por marcelojs » Ter Jun 11, 2013 23:43
- 0 Respostas
- 1671 Exibições
- Última mensagem por marcelojs

Ter Jun 11, 2013 23:43
Análise Combinatória
-
- Questão Banco do Brasil 2011 - Dúvida Urgente
por Tay » Qui Mar 28, 2013 13:31
- 3 Respostas
- 2565 Exibições
- Última mensagem por Tay

Sáb Mar 30, 2013 17:26
Matemática Financeira
-
- questão urgente - TIR
por sirle ignes » Seg Mar 29, 2010 18:22
- 0 Respostas
- 1280 Exibições
- Última mensagem por sirle ignes

Seg Mar 29, 2010 18:22
Matemática Financeira
-
- Resolver questão urgente.
por Androcles Lima Souza » Sex Nov 27, 2009 13:42
- 0 Respostas
- 982 Exibições
- Última mensagem por Androcles Lima Souza

Sex Nov 27, 2009 13:42
Matemática Financeira
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Princípio da Indução Finita
Autor:
Fontelles - Dom Jan 17, 2010 14:42
Não sei onde este tópico se encaixaria. Então me desculpem.
Eu não entendi essa passagem, alguém pode me explicar?

O livro explica da seguinte forma.
1°) P(1) é verdadeira, pois

2°) Admitamos que

, seja verdadeira:

(hipótese da indução)
e provemos que

Temos: (Nessa parte)

Assunto:
Princípio da Indução Finita
Autor:
MarceloFantini - Seg Jan 18, 2010 01:55
Boa noite Fontelles.
Não sei se você está familiarizado com o
Princípio da Indução Finita, portanto vou tentar explicar aqui.
Ele dá uma equação, no caso:

E pergunta: ela vale para todo n? Como proceder: no primeiro passo, vemos se existe pelo menos um caso na qual ela é verdadeira:

Portanto, existe pelo menos um caso para o qual ela é verdadeira. Agora, supomos que

seja verdadeiro, e pretendemos provar que também é verdadeiro para

.




Daí pra frente, ele usou o primeiro membro para chegar em uma conclusão que validava a tese. Lembre-se: nunca saia da tese.
Espero ter ajudado.
Um abraço.
Assunto:
Princípio da Indução Finita
Autor:
Fontelles - Seg Jan 18, 2010 02:28
Mas, Fantini, ainda fiquei em dúvida na passagem que o autor fez (deixei uma msg entre o parêntese).
Obrigado pela ajuda, mesmo assim.
Abraço!
Assunto:
Princípio da Indução Finita
Autor:
Fontelles - Qui Jan 21, 2010 11:32
Galera, ajuda aí!
Por falar nisso, alguém conhece algum bom material sobre o assunto. O livro do Iezzi, Matemática Elementar vol. 1 não está tão bom.
Assunto:
Princípio da Indução Finita
Autor:
MarceloFantini - Qui Jan 21, 2010 12:25
Boa tarde Fontelles!
Ainda não estou certo de qual é a sua dúvida, mas tentarei novamente.
O que temos que provar é isso:

, certo? O autor começou do primeiro membro:

Isso é verdadeiro, certo? Ele apenas aplicou a distributiva. Depois, partiu para uma desigualdade:

Que é outra verdade. Agora, com certeza:

Agora, como

é

a

, e este por sua vez é sempre

que

, logo:

Inclusive, nunca é igual, sempre maior.
Espero (dessa vez) ter ajudado.
Um abraço.
Assunto:
Princípio da Indução Finita
Autor:
Caeros - Dom Out 31, 2010 10:39
Por curiosidade estava estudando indução finita e ao analisar a questão realmente utilizar a desigualdade apresentada foi uma grande sacada para este problema, só queria tirar uma dúvida sobre a sigla (c.q.d), o que significa mesmo?
Assunto:
Princípio da Indução Finita
Autor:
andrefahl - Dom Out 31, 2010 11:37
c.q.d. = como queriamos demonstrar =)
Assunto:
Princípio da Indução Finita
Autor:
Abelardo - Qui Mai 05, 2011 17:33
Fontelles, um bom livro para quem ainda está ''pegando'' o assunto é:'' Manual de Indução Matemática - Luís Lopes''. É baratinho e encontras na net com facilidade. Procura também no site da OBM, vais encontrar com facilidade material sobre PIF... em alguns sites que preparam alunos para colégios militares em geral também tem excelentes materiais.
Assunto:
Princípio da Indução Finita
Autor:
MarceloFantini - Qui Mai 05, 2011 20:05
Abelardo, faz 1 ano que o Fontelles não visita o site, da próxima vez verifique as datas.
Assunto:
Princípio da Indução Finita
Autor:
Vennom - Qui Abr 26, 2012 23:04
MarceloFantini escreveu:Abelardo, faz 1 ano que o Fontelles não visita o site, da próxima vez verifique as datas.
Rpz, faz um ano que o fulano não visita o site, mas ler esse comentário dele enquanto respondia a outro tópico me ajudou. hAUEhUAEhUAEH obrigado, Marcelo. Sua explicação de indução finita me sanou uma dúvida sobre outra coisa.

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



 com a roda traseira?
com a roda traseira?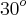 ;
; do círculo descrito pela roda dianteira;
do círculo descrito pela roda dianteira; do círculo descrito pela roda traseira é o cateto adjacente ao ângulo de
do círculo descrito pela roda traseira é o cateto adjacente ao ângulo de 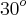 , no mesmo triângulo;
, no mesmo triângulo; e
e  com seno e tangente, respectivamente;
com seno e tangente, respectivamente; metros
metros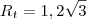 metros
metros



 e
e 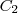 possuem raio de mesma medida ("Um ciclista pedala uma bicicleta com rodas de mesmo diâmetro...").
possuem raio de mesma medida ("Um ciclista pedala uma bicicleta com rodas de mesmo diâmetro..."). ("...com distância entre os eixos de 1,20m...").
("...com distância entre os eixos de 1,20m..."). :
: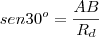
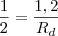
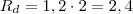 metros
metros :
: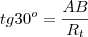

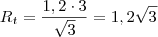 metros
metros



 , seja verdadeira:
, seja verdadeira: (hipótese da indução)
(hipótese da indução)



 seja verdadeiro, e pretendemos provar que também é verdadeiro para
seja verdadeiro, e pretendemos provar que também é verdadeiro para  .
.



 , certo? O autor começou do primeiro membro:
, certo? O autor começou do primeiro membro:


 é
é  a
a  , e este por sua vez é sempre
, e este por sua vez é sempre  que
que  , logo:
, logo:
