Olá,
Estou em dúvida na seguinte questão:
"Em um trecho reto e plano de uma praia, um topógrafo que está situado
em uma rocha (ponto B) observa uma árvore à beira de uma ilha (ponto A).
Para estimar a distância entre essa ilha e a praia, ele usa um teodolito,
instrumento de medição de ângulos. Primeiramente, ele se situa no
ponto B e mede um ângulo de 90º entre a praia e a linha de visão da árvore.
Depois disso, ele sai do ponto B, desloca-se em linha reta 160 metros pela
praia e mede, de um ponto C, um ângulo de 50º também entre a praia e a
linha de visão da árvore, conforme a figura.
Considerando que essa parte da praia se situa no mesmo nível que a ilha, a
distância da rocha (ponto B) até a árvore usada como referencial (ponto A)
é, em metros,
(A) 250.
(B) 230.
(C) 210.
(D) 190.
(E) 170. "
Eu fiz por COS 50° = 160 / x
e o resultado de x = 250
Mas no gabarito, a resposta é 190. Não consigo entender o porquê.
Obrigada.
http://fatweb.s3.amazonaws.com/vestibul ... _Prova.pdf (questão 31)
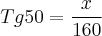
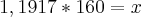
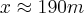
por ![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png "{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}")
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png "{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}")
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png "{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}")
da seguinte forma:
.
da seguinte forma:
.