há mais de um mês tento conseguir uma solução para o problema abaixo . por favor , se alguém puder me ajudar com a solução ou pelo menos com uma dica , ficarei muito agradecido.
seja E um ponto interior de um quadrado ABCD , de modo que AE=c, BE=a e CE=a + b, onde a² + b² = c² . A medida do ângulo BÊC é igual a :
a)30º
b)45º
c)60º
d)90º
e)120º
f)135º


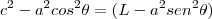
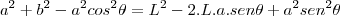
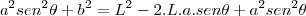
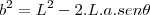
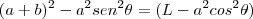
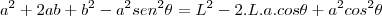
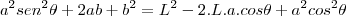
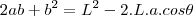
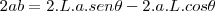
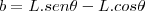
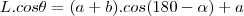
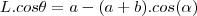
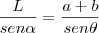
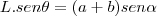

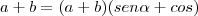
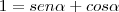
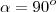

![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)