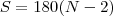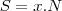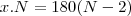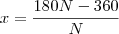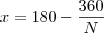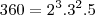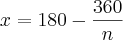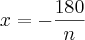por Jhennyfer » Ter Abr 09, 2013 19:48
por Jhennyfer » Ter Abr 09, 2013 19:48
Não quero a resolução... quero apenas informações para que eu possa fazer o calculo...
- Sabe-se que a medida, em graus, de cada ângulo interno de um poligono convexo regular é expressa por um número inteiro. Sendo N o número de lados dos poligonos que satisfazem essa condição, determine a quantidade de valores que N pode assumir.
-
Jhennyfer
- Usuário Parceiro

-
- Mensagens: 67
- Registrado em: Sáb Mar 30, 2013 15:19
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por young_jedi » Qua Abr 10, 2013 15:51
por young_jedi » Qua Abr 10, 2013 15:51
se ele tem N lados ele tambem tem N angulos internos a soma dos angulo internos portanto é
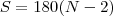
mais temos que se trata de poligono regular então seus angulos são iguais portanto se eles mede x temos que
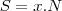
e finalemnte
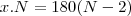
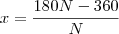
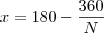
como x deve ser um valor inteiro então a divisão de 360 por N deve ser um valor inteiro e maior que 2 para que x não seja 0
decompondo 360 em fatores primos temos
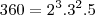
tente encontrar os valores de N e comente
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por Jhennyfer » Sex Abr 12, 2013 23:40
por Jhennyfer » Sex Abr 12, 2013 23:40
Boom, eu compreendi pouca coisa... entendi a linha de raciocinio..
porém, não estou conseguindo concluir a questão.
Enfim...
No final vc colocou que:
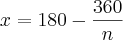
Mas ali não deveria continuar? tirar o mmc? assim...
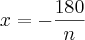
E porque tem que decompor o 360?
Li e reeli meu material e não achei nada que pudesse me ajudar.
Já fiz um monte de calculo aqui e to beem perdida, acho q já nem sei o que "tô" fazendo!
-
Jhennyfer
- Usuário Parceiro

-
- Mensagens: 67
- Registrado em: Sáb Mar 30, 2013 15:19
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por young_jedi » Sex Abr 12, 2013 23:58
por young_jedi » Sex Abr 12, 2013 23:58
quando voce chega nessa relação
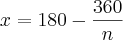
voce ja sabe que x tem que ser um valor inteiro então o n tem que ser um dos divisores de 360, logo voce tem que encontrar os divisores de 360, eu fiz a decomposição do 360 por que assim fica mais facil fisualizar quais são seus divisores
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
Voltar para Geometria Plana
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Ângulo para um dado arco e raio] Dedução e compreensão.
por Matheus Lacombe O » Dom Nov 11, 2012 21:49
- 3 Respostas
- 3290 Exibições
- Última mensagem por MarceloFantini

Seg Nov 12, 2012 19:53
Trigonometria
-
- Ajuda com exercicio!!!
por tuany » Seg Mar 24, 2008 15:34
- 3 Respostas
- 4117 Exibições
- Última mensagem por tuany

Ter Mar 25, 2008 16:50
Funções
-
- Ajuda com exercicio!!!
por karol_agnelli » Qua Mar 26, 2008 19:40
- 6 Respostas
- 7267 Exibições
- Última mensagem por Cleyson007

Qua Jun 10, 2009 15:23
Tópicos sem Interação (leia as regras)
-
- ajuda com o exercicio
por Mimizinha » Seg Mar 31, 2008 18:19
- 2 Respostas
- 3491 Exibições
- Última mensagem por Mimizinha

Ter Abr 01, 2008 10:24
Geometria Plana
-
- Ajuda em Exercício.
 por Levi23 » Dom Set 28, 2008 02:01
por Levi23 » Dom Set 28, 2008 02:01
- 12 Respostas
- 8819 Exibições
- Última mensagem por admin

Sáb Out 04, 2008 13:51
Trigonometria
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.