 por alex_08 » Seg Fev 11, 2013 18:00
por alex_08 » Seg Fev 11, 2013 18:00
Questão 1: Num triângulo ABC, as bissetrizes dos ângulos externos em B e C formam
um ângulo de 40º e a altura relativa ao lado BC forma com a bissetriz do ângulo A um ângulo de
25º. Calcule os ângulos do trângulo.
Questão 2: ABC �e um triângulo no qual a bissetriz interna relativa ao ângulo  �é igual
ao lado AB e a bissetriz interna relativa ao ângulo C �e igual ao lado AC. Calcule os ângulos do
triângulo ABC, representando-os em graus, minutos e segundos.
Obrigado.
-
alex_08
- Usuário Dedicado

-
- Mensagens: 29
- Registrado em: Dom Fev 10, 2013 01:29
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matematica
- Andamento: cursando
 por alex_08 » Qui Fev 14, 2013 11:24
por alex_08 » Qui Fev 14, 2013 11:24
Bom Dia, pessoal conseguir resolver a questão 1. Obrigado
Quem puder me ajudar com a Questão 2, ficaria grato.
abraços.
-
alex_08
- Usuário Dedicado

-
- Mensagens: 29
- Registrado em: Dom Fev 10, 2013 01:29
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matematica
- Andamento: cursando
 por young_jedi » Qui Fev 14, 2013 13:52
por young_jedi » Qui Fev 14, 2013 13:52
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por alex_08 » Qui Fev 14, 2013 18:46
por alex_08 » Qui Fev 14, 2013 18:46
muito obrigado.
-
alex_08
- Usuário Dedicado

-
- Mensagens: 29
- Registrado em: Dom Fev 10, 2013 01:29
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matematica
- Andamento: cursando
 por alex_08 » Ter Fev 26, 2013 09:43
por alex_08 » Ter Fev 26, 2013 09:43
como eu divido?
900º/13
1080º/13
360º/13?
pode me ajudar?
-
alex_08
- Usuário Dedicado

-
- Mensagens: 29
- Registrado em: Dom Fev 10, 2013 01:29
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matematica
- Andamento: cursando
 por young_jedi » Ter Fev 26, 2013 14:28
por young_jedi » Ter Fev 26, 2013 14:28
voce faz a divisão normal, o numero depoies da virgula multiplicado por 60 dara os minutos, se ainda tiver valor depois da virgula esse valor multiplicado por 60 dara os segundos
exemplo

portanto temos 69º
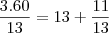
então temos 13'

portanto temos 50"
ou seja o angulo é
69º 13' 50"
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por alex_08 » Ter Fev 26, 2013 16:20
por alex_08 » Ter Fev 26, 2013 16:20
muito obrigado.

-
alex_08
- Usuário Dedicado

-
- Mensagens: 29
- Registrado em: Dom Fev 10, 2013 01:29
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matematica
- Andamento: cursando
Voltar para Geometria Plana
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Geometria Plana] questões
 por Micael » Qua Mar 13, 2013 00:04
por Micael » Qua Mar 13, 2013 00:04
- 2 Respostas
- 1438 Exibições
- Última mensagem por Micael

Qui Mar 14, 2013 09:12
Geometria Plana
-
- [Geometria Plana] questões
 por Micael » Seg Mar 18, 2013 18:23
por Micael » Seg Mar 18, 2013 18:23
- 3 Respostas
- 1835 Exibições
- Última mensagem por timoteo

Seg Mar 18, 2013 19:15
Geometria Plana
-
- Duas questões de Geometria.
por JoaoGabriel » Dom Set 26, 2010 09:34
- 4 Respostas
- 7856 Exibições
- Última mensagem por JoaoGabriel

Dom Set 26, 2010 14:49
Geometria Plana
-
- [Geometria paralelogramo] Ajuda questões
por imabr » Dom Jun 24, 2012 23:12
- 1 Respostas
- 1617 Exibições
- Última mensagem por MarceloFantini

Seg Jun 25, 2012 01:29
Geometria Analítica
-
- Duvidas em algumas questões de geometria analítica.
por sphinx » Ter Mar 05, 2013 16:46
- 4 Respostas
- 3018 Exibições
- Última mensagem por Russman

Ter Mar 05, 2013 22:28
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


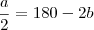
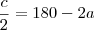
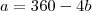

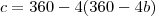


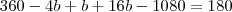





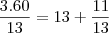


 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.