 por Mariana Martin » Qua Set 12, 2012 12:16
por Mariana Martin » Qua Set 12, 2012 12:16
Calcular a mediana CM de um triângulo retângulo ABC, sabendo que a hipotenusa BC=8cm e o cateto AC=3cm.
A minha dúvida nesse exercício é saber quando a mediana intercepta com ângulo de 90º e também como posso calculá-la. Estou sem norte, se vocês puderem me ajudar...
Obrigada, pessoal.
-
Mariana Martin
- Usuário Dedicado

-
- Mensagens: 27
- Registrado em: Qui Jun 21, 2012 15:10
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por young_jedi » Qua Set 12, 2012 13:09
por young_jedi » Qua Set 12, 2012 13:09
Não sei se entendi bem sua duvida mais o enunciado do seu problema pelo que entendi podem ser representado pela figura:
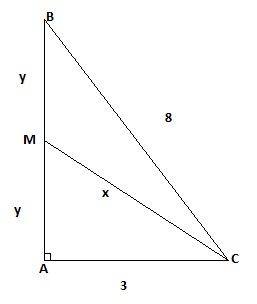
- Triangulo retangula
- triangulo_mediana.jpg (9.77 KiB) Exibido 2045 vezes
assim por pitagoras voce calcula y:
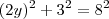
e depois x
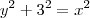
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por Mariana Martin » Qua Set 12, 2012 13:37
por Mariana Martin » Qua Set 12, 2012 13:37
Entendi, eu estava montando o desenho de forma errada. Mas por exemplo, tem como a mediana, onde ela intercepta, ser 90°? No caso, CM intercepta a aresta y, nesse ponto é possível formar 90°? Ou a mediana nunca forma 90°?
-
Mariana Martin
- Usuário Dedicado

-
- Mensagens: 27
- Registrado em: Qui Jun 21, 2012 15:10
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por young_jedi » Qua Set 12, 2012 14:34
por young_jedi » Qua Set 12, 2012 14:34
É possivel em um triangulo isoceles:
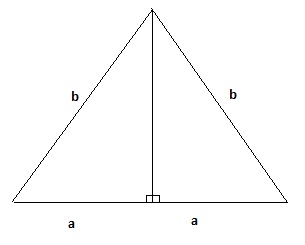
- Triangulo isoceles
- triangulo_isoceles.jpg (8.45 KiB) Exibido 2042 vezes
Em um trigangulo retangulo so é possivel a mediana com relação a hipotenusa com relação aos catetos nao
pois se o angulo for 90º a mediana sera paralela ao outro cateto e isso é impossivel
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por Mariana Martin » Qua Set 12, 2012 21:26
por Mariana Martin » Qua Set 12, 2012 21:26
Entendi, obrigada.
-
Mariana Martin
- Usuário Dedicado

-
- Mensagens: 27
- Registrado em: Qui Jun 21, 2012 15:10
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
Voltar para Geometria Plana
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Mediana]
por MarciaZardo » Sáb Jan 21, 2012 17:46
- 2 Respostas
- 1772 Exibições
- Última mensagem por MarciaZardo

Dom Jan 22, 2012 20:24
Estatística
-
- mediana
por alfabeta » Seg Mar 05, 2012 11:45
- 5 Respostas
- 3410 Exibições
- Última mensagem por LuizAquino

Seg Mar 05, 2012 22:45
Geometria Plana
-
- Mediana
por Pri Ferreira » Seg Abr 09, 2012 16:17
- 1 Respostas
- 1609 Exibições
- Última mensagem por LuizAquino

Ter Abr 10, 2012 20:55
Estatística
-
- Mediana e a Moda
por Walquiria » Dom Dez 18, 2011 12:14
- 0 Respostas
- 905 Exibições
- Última mensagem por Walquiria

Dom Dez 18, 2011 12:14
Estatística
-
- Mediana de classes
por ah001334 » Ter Mar 06, 2012 08:54
- 0 Respostas
- 1192 Exibições
- Última mensagem por ah001334

Ter Mar 06, 2012 08:54
Estatística
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Simplifique a expressão com radicais duplos
Autor:
Balanar - Seg Ago 09, 2010 04:01
Simplifique a expressão com radicais duplos abaixo:
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
Resposta:
Dica:
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
(dica : igualar a expressão a

e elevar ao quadrado os dois lados)
Assunto:
Simplifique a expressão com radicais duplos
Autor:
MarceloFantini - Qua Ago 11, 2010 05:46
É só fazer a dica.
Assunto:
Simplifique a expressão com radicais duplos
Autor:
Soprano - Sex Mar 04, 2016 09:49
Olá,
O resultado é igual a 1, certo?
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


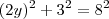
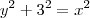

![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)