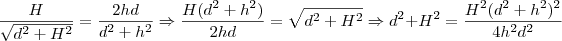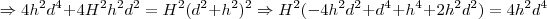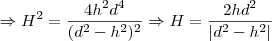(ITA) - Um dispositivo colocado no solo a uma distância d de uma torre dispara dois projéteis em trajetórias retilíneas. O primeiro, lançado sob um ângulo
 ?
?  , atinge a torre a uma altura h. Se o segundo, disparado sob um ângulo 2
, atinge a torre a uma altura h. Se o segundo, disparado sob um ângulo 2 , atinge-a a uma altura H, a relação entre as duas alturas será:
, atinge-a a uma altura H, a relação entre as duas alturas será:a) H =
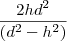
b) H =
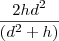
c) H =

d) H =
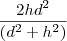
e) H =

Bom, tentei resolver aqui, mas acabei emperrando. Vou colocar um desenho pra facilitar o entendimento do meu raciocínio:
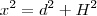
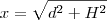
e


Além disso:
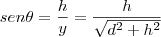
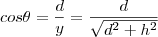
Por fim:
 >>>>>>>>>>>>
>>>>>>>>>>>> 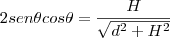
Aí, eu substituo os valores de
 e
e  , entretanto ,não tenho como isolar o H. Ficaria assim:
, entretanto ,não tenho como isolar o H. Ficaria assim: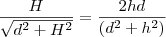
Não consigo isolar o H, entendem. Alguém pode ajudar?