 por Pri Ferreira » Sex Mai 18, 2012 23:32
por Pri Ferreira » Sex Mai 18, 2012 23:32
Num triângulo retângulo, a medida de um cateto é a metade da medida da hipotenusa. O quociente da medida
do outro cateto pela medida da hipotenusa é:
A)

B)
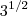
C)
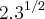
D)
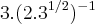
E) N.R.A.
Tentei mas aind não cheguei no resultado!!
Ajuda.
-
Pri Ferreira
- Usuário Parceiro

-
- Mensagens: 59
- Registrado em: Qua Out 19, 2011 20:53
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática
- Andamento: formado
 por pedroaugustox47 » Sáb Mai 19, 2012 02:23
por pedroaugustox47 » Sáb Mai 19, 2012 02:23
-
pedroaugustox47
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Sex Mai 11, 2012 01:53
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Sistema Elite de Ensino-CN/EPCAR
- Andamento: cursando
 por DanielFerreira » Sáb Mai 19, 2012 12:54
por DanielFerreira » Sáb Mai 19, 2012 12:54
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por Pri Ferreira » Seg Mai 21, 2012 22:31
por Pri Ferreira » Seg Mai 21, 2012 22:31
Obrigada, pela ajuda, mas a resposta do gabarito é D.
Não seria nenhuma das opções dadas...
-
Pri Ferreira
- Usuário Parceiro

-
- Mensagens: 59
- Registrado em: Qua Out 19, 2011 20:53
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática
- Andamento: formado
 por pedroaugustox47 » Seg Mai 21, 2012 22:45
por pedroaugustox47 » Seg Mai 21, 2012 22:45
Pri Ferreira escreveu:Obrigada, pela ajuda, mas a resposta do gabarito é D.
Não seria nenhuma das opções dadas...
note que
![\left[3.(2.\sqrt[]{3})^\left(-1 \right) \right]=\left[3.(\frac{1}{2. \sqrt[]{3}}) \right]=\left[ \frac{3}{2.\sqrt[]{3}}\right]=\left[\frac{3.\sqrt[]{3}}{6} \right]=\frac{\sqrt[]{3}}{2} \left[3.(2.\sqrt[]{3})^\left(-1 \right) \right]=\left[3.(\frac{1}{2. \sqrt[]{3}}) \right]=\left[ \frac{3}{2.\sqrt[]{3}}\right]=\left[\frac{3.\sqrt[]{3}}{6} \right]=\frac{\sqrt[]{3}}{2}](/latexrender/pictures/b86994e635de8ff615f735c0da415e26.png)
-
pedroaugustox47
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Sex Mai 11, 2012 01:53
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Sistema Elite de Ensino-CN/EPCAR
- Andamento: cursando
 por Pri Ferreira » Seg Mai 21, 2012 22:48
por Pri Ferreira » Seg Mai 21, 2012 22:48
Ah!!Agora visualizei!!Obrigada!!!
-
Pri Ferreira
- Usuário Parceiro

-
- Mensagens: 59
- Registrado em: Qua Out 19, 2011 20:53
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática
- Andamento: formado
Voltar para Geometria Plana
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Calculos envolvendo triângulo retângulo e retângulo
 por andersontricordiano » Seg Abr 18, 2011 02:29
por andersontricordiano » Seg Abr 18, 2011 02:29
- 1 Respostas
- 4034 Exibições
- Última mensagem por MarceloFantini

Seg Abr 18, 2011 04:19
Progressões
-
- Triangulo Retangulo
por ginrj » Qui Jun 04, 2009 18:56
- 1 Respostas
- 3409 Exibições
- Última mensagem por ginrj

Seg Jun 15, 2009 18:14
Geometria Plana
-
- Triângulo retângulo
por DanielFerreira » Qua Jul 29, 2009 15:38
- 5 Respostas
- 6826 Exibições
- Última mensagem por Cleyson007

Qui Jul 30, 2009 17:22
Trigonometria
-
- Triângulo retangulo
por cristina » Seg Set 21, 2009 14:56
- 3 Respostas
- 2203 Exibições
- Última mensagem por DanielFerreira

Ter Set 22, 2009 14:18
Trigonometria
-
- Triângulo retângulo
por DanielFerreira » Qui Mar 03, 2011 11:26
- 1 Respostas
- 2122 Exibições
- Última mensagem por Elcioschin

Qui Mar 03, 2011 14:43
Geometria Plana
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.

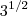
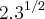
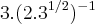


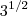
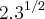
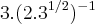

 = Senx
= Senx
![\frac{cateto .adjacente (o. outro. cateto)}{hipotenusa}=Cos30=\frac{\sqrt[2]{3}}{2} \frac{cateto .adjacente (o. outro. cateto)}{hipotenusa}=Cos30=\frac{\sqrt[2]{3}}{2}](/latexrender/pictures/0cd673403c1ac06b7ccfaf43f47ae1cb.png)


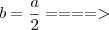
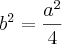

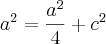
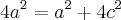


![\frac{c}{a} = \sqrt[]{\left(\frac{3}{4} \right)} \frac{c}{a} = \sqrt[]{\left(\frac{3}{4} \right)}](/latexrender/pictures/857ef5685ce883d210cc45df616b827e.png)
![\frac{c}{a} = \frac{\sqrt[]{3}}{2} \frac{c}{a} = \frac{\sqrt[]{3}}{2}](/latexrender/pictures/7a73e9f008a798e848061982286986b4.png)


![\left[3.(2.\sqrt[]{3})^\left(-1 \right) \right]=\left[3.(\frac{1}{2. \sqrt[]{3}}) \right]=\left[ \frac{3}{2.\sqrt[]{3}}\right]=\left[\frac{3.\sqrt[]{3}}{6} \right]=\frac{\sqrt[]{3}}{2} \left[3.(2.\sqrt[]{3})^\left(-1 \right) \right]=\left[3.(\frac{1}{2. \sqrt[]{3}}) \right]=\left[ \frac{3}{2.\sqrt[]{3}}\right]=\left[\frac{3.\sqrt[]{3}}{6} \right]=\frac{\sqrt[]{3}}{2}](/latexrender/pictures/b86994e635de8ff615f735c0da415e26.png)

