Conceitos de pontos notáveis em triângulo

[alfabeta]

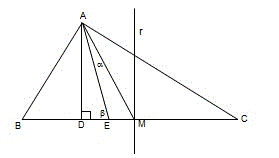
No triângulo ABC da figura abaixo, os segmentos AD e BC são perpendiculares, os ângulos BÂE e EÂC são iguais, as medidas dos segmentos BM e MC são iguais e r é uma reta perpendicular ao segmento BC, passando por M.



Com base nessas informações, julgue os itens:
01) Os triângulos ABM e AMC têm áreas iguais.
02) O centro da circunferência que circunscreve o triângulo ABC pertence à reta r.
03) a.senbeta = b.sen(alfa), onde a e b indicam as medidas dos segmentos EM e AM, respectivamente.
04) O raio da circunferência que circunscreve o triângulo ABD mede um terço da medida do lado AB.

Tentativa:
01) verdadeira, pois são divididos pela mediana. Mas como provo isto?
E as outras não sei fazer.

[LuizAquino]

No triângulo ABC da figura abaixo, os segmentos AD e BC são perpendiculares, os ângulos BÂE e EÂC são iguais, as medidas dos segmentos BM e MC são iguais e r é uma reta perpendicular ao segmento BC, passando por M.

triangulo.gif (3.25 KiB) Exibido 1778 vezes

Com base nessas informações, julgue os itens:
01) Os triângulos ABM e AMC têm áreas iguais.
02) O centro da circunferência que circunscreve o triângulo ABC pertence à reta r.
03) a.senbeta = b.sen(alfa), onde a e b indicam as medidas dos segmentos EM e AM, respectivamente.
04) O raio da circunferência que circunscreve o triângulo ABD mede um terço da medida do lado AB.

Tentativa:
01) verdadeira, pois são divididos pela mediana. Mas como provo isto?
E as outras não sei fazer.

Note que tanto ABM quanto AMC possuem a mesma medida para a altura e a mesma medida para a base.

02) O centro da circunferência que circunscreve o triângulo ABC pertence à reta r.

Veja a definição de circuncentro:
http://pt.wikipedia.org/wiki/Tri%C3%A2ngulo#Mediatriz

03) a.senbeta = b.sen(alfa), onde a e b indicam as medidas dos segmentos EM e AM, respectivamente.

Veja a Lei dos Senos:
http://pt.wikipedia.org/wiki/Lei_dos_senos

04) O raio da circunferência que circunscreve o triângulo ABD mede um terço da medida do lado AB.

Faça uma pesquisa sobre a relação que existe entre a hipotenusa de um triângulo retângulo e o diâmetro da circunferência que circunscreve esse triângulo retângulo.