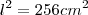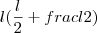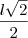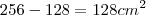por Arkanus Darondra » Qua Fev 01, 2012 12:00
por Arkanus Darondra » Qua Fev 01, 2012 12:00
Olá Hugo.
Por favor, redija seus textos quando for postar. Apenas em imagens aquilo que for necessário.
Isso porque se o seu texto não estiver escrito, as pessoas não encontraram uma dúvida já sanada aqui no fórum por meio do mecanismo de busca.
J Hugo escreveu:De uma lâmina quadrada de metal corta-se uma peça circular do maior tamanho possível, e desta corta-se um quadrado, também do maior
tamanho possível. Se o lado do quadrado original mede 16 cm, a área da superfície do metal que foi desperdiçado, em centímetros quadrados, é:

A área desperdiçada é aquela que não foi usada para obter o quadrado JMNP (Verde)
Área do quadrado ABCD (Preto): 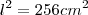 Área do quadrado JMNP (Verde):
Área do quadrado JMNP (Verde):Temos que sua diagonal (azul) vale
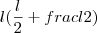
Por pitágoras, seu lado vale
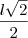
Sua área:

Então o desperdício foi de
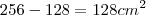
J Hugo escreveu:Se o hexágono regular da figura tem área 2, a área do pentágono assinalado é


Vemos que a área total do hexágono vale 6 área do triângulo destacado
Logo, a área do pentagono

-
Arkanus Darondra
- Colaborador Voluntário

-
- Mensagens: 187
- Registrado em: Seg Dez 26, 2011 18:19
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Geometria Plana
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.