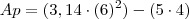por maria cleide » Sáb Ago 27, 2011 15:35
por maria cleide » Sáb Ago 27, 2011 15:35
Babucha, uma cabra, está amarrada em em canto de um barracão de base retangular. Ela está com tanta fome que já esticou a corda até o máximo, tentando pastar na melhor parte do terreno. Se o barracão, que está fechado, tem 5m por 4m e a corda tem 6m, qual é a área aproximada, em torno do barracão, em que Babucha poderá pastar?
Considere 
A.( )
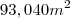
B.( )
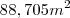
C.( )

D.( )
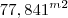
Área total: 113,04
Percebi que se dividir a circunferencia em 4, ela poderá pastae em três quartos desta circunferência, o equivalente a

, mas não sei continuar.
- Anexos
-

-
maria cleide
- Usuário Parceiro

-
- Mensagens: 54
- Registrado em: Dom Mai 08, 2011 12:57
- Formação Escolar: ENSINO FUNDAMENTAL I
- Andamento: cursando
 por Caradoc » Sáb Ago 27, 2011 17:41
por Caradoc » Sáb Ago 27, 2011 17:41
Você tem que considerar as dimensões do barracão.
A cabra poderá pastar em todo o círculo de raio 6 m, menos na parte onde fica o barracão, ou seja, um retângulo de 5 m por 4 m.
Analisando mais precisamente, haveria um pedacinho do barracão que ficaria para fora do círculo, mas como o exercício pede uma área aproximada, então temos que a área da pastagem é a área do círculo menos a área do barraco:

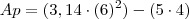

-
Caradoc
- Usuário Dedicado

-
- Mensagens: 37
- Registrado em: Qui Dez 16, 2010 17:17
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
Voltar para Geometria Plana
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.

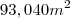
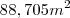

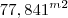
 , mas não sei continuar.
, mas não sei continuar.

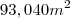
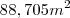

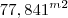
 , mas não sei continuar.
, mas não sei continuar.