A entrada de um ginásio de esportes tem o formato de um arco de parábola sustentado por 4 colunas AB, CD, EF e GH, conforme figura abaixo. As colunas AB e GH têm 3 metros de comprimento cada e a distância entre elas é de 18 metros. CD tem 8 m de comprimento e EF tem 11 m. Se a coluna CD está a 3 m de AB, pode-se afirmar que a coluna EF encontra-se distante de AB
A) 8 metros.
B) 9 metros.
C) 10 metros.
D) 11 metros.
E) 12 metros.
Eu resolvi esse problema e encontrei a solução 10 e o gabarito do mesmo me diz que é 12m eu gostaria de sua ajuda.
Obrigado antecipadamente.


 e através do ponto
e através do ponto 

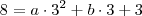



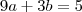


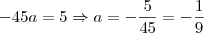
 .
.


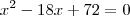



 .
.



