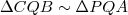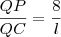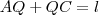por Joan » Sex Jul 22, 2011 18:42
por Joan » Sex Jul 22, 2011 18:42
ABC é um triângulo equilátero. Seja P um ponto do plano de ABC e exterior ao triângulo de tal forma que PB intersecta AC em Q(Q está entre A e C). Sabendo que o Ângulo APB é igual a 60º, que PA = 6 e PC = 8, a medida de PQ será?...bem eu fiz o desenho do enunciado que verão na figura, e nao consigo imaginar mais nada.
 http://imageshack.us/photo/my-images/808/questo3.png/
http://imageshack.us/photo/my-images/808/questo3.png/desde já grato.
-
Joan
- Usuário Ativo

-
- Mensagens: 12
- Registrado em: Sex Jul 22, 2011 18:07
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por FilipeCaceres » Sex Jul 22, 2011 20:09
por FilipeCaceres » Sex Jul 22, 2011 20:09
Olá Joan,
Vou lhe pedir para usar as ferramentas do fórum para postar suas figuras, veja que é simples, basta você clicar em Anexar Arquivo que fica na parte inferior esquerdo, coloquei sua figura anexada abaixo.

- CN2010.GIF (7.25 KiB) Exibido 3709 vezes
Como você já fez a figura agora basta fazer o seguinte:
1º) Faça a semelhança


2º) Faça a semelhança
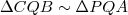
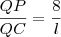
Isolando AQ e QC e substituindo em:
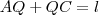
Você encontrará a resposta

Abraço.
-
FilipeCaceres
- Colaborador Voluntário

-
- Mensagens: 351
- Registrado em: Dom Out 31, 2010 21:43
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Tec. Mecatrônica
- Andamento: formado
 por Joan » Sáb Jul 23, 2011 01:03
por Joan » Sáb Jul 23, 2011 01:03
FilipeCaceres escreveu:Olá Joan,
Vou lhe pedir para usar as ferramentas do fórum para postar suas figuras, veja que é simples, basta você clicar em Anexar Arquivo que fica na parte inferior esquerdo, coloquei sua figura anexada abaixo.
CN2010.GIF
Como você já fez a figura agora basta fazer o seguinte:
1º) Faça a semelhança


2º) Faça a semelhança
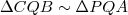
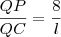
Isolando AQ e QC e substituindo em:
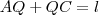
Você encontrará a resposta

Abraço.
Amigo desde já obrigado...
mais vc faz multiplicação crusada?? para achar??
desculpe-me se a pergunta for idiota amigo mais preciso muito aprender...
desde já muitissimo grato.
-
Joan
- Usuário Ativo

-
- Mensagens: 12
- Registrado em: Sex Jul 22, 2011 18:07
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Joan » Sáb Jul 23, 2011 11:34
por Joan » Sáb Jul 23, 2011 11:34
Obrigado. Consegui.
-
Joan
- Usuário Ativo

-
- Mensagens: 12
- Registrado em: Sex Jul 22, 2011 18:07
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Geometria Plana
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [conjunto solução em R] Questão Colégio Naval 2010
por Joan » Sáb Jul 23, 2011 12:06
- 2 Respostas
- 5386 Exibições
- Última mensagem por Joan

Sáb Jul 23, 2011 13:21
Equações
-
- [triângulo / segmento] Ajuda em mais uma do colegio naval...
 por Joan » Sáb Jul 23, 2011 13:18
por Joan » Sáb Jul 23, 2011 13:18
- 6 Respostas
- 4656 Exibições
- Última mensagem por Joan

Seg Jul 25, 2011 16:11
Geometria Plana
-
- MMC e MDC - Colégio Naval
por igorcamilo » Sáb Jun 25, 2011 21:22
- 1 Respostas
- 2029 Exibições
- Última mensagem por FilipeCaceres

Dom Jun 26, 2011 16:13
Álgebra Elementar
-
- Colégio Naval
por Joan » Seg Jul 25, 2011 16:38
- 8 Respostas
- 8322 Exibições
- Última mensagem por LuizAquino

Ter Jul 26, 2011 21:35
Álgebra Elementar
-
- Divisibilidade - Colégio naval
por igorcamilo » Sex Jun 24, 2011 19:22
- 2 Respostas
- 2459 Exibições
- Última mensagem por igorcamilo

Sex Jun 24, 2011 20:32
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.