Se cada lado de um quadrado é acrescido de 6 cm; sua área aumenta de 108 cm2. Nessas condições, a área do quadrado
original é:
O meu raciocínio foi o seguinte:
(x+6)*(x+6)= 108
x²+6x+6x+36=180
x²+12x-72=0
Delta= 12²-4*1*(-72)
D=144+288
D=432 ou 3*144
Acho que consegui compreender veja o meu reciocínio após a sua ajuda:
x=-12+-raiz de 3*144/2*1
x=-12+-raiz de 3*12/2
x=-12+-raiz de 36/2
x=-12+-6/2
x1=-12+6/2=>-6/2=-3
x2=-12-6/2=>-18/2=-9
S= {-3;-9} estou certo até aqui?
Encontrei uma resposta em um site e gostaria de saber se ela está pertinente:
( x + 6 )² = x² + 108
x² + 12x + 36 = x² + 108
12x = 72
x = 6
.
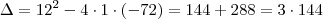
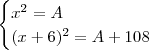
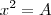e 
, e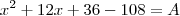stá certo. Logo: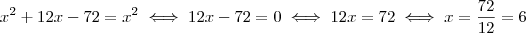
Talvez tenha errado apenas na hora de mostrar aqui.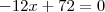
e não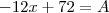 
, como você fez. Na passagem seguinte você conserta isso e faz 
como se fosse zero e não A, mas é bom apontar o erro.
por ![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png "\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}")
![\sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png "\sqrt[]{2}")
e elevar ao quadrado os dois lados)