Tem um exrcício aki numa das minhas listas que pede para eu verificar que as equações dadas são de uma circunferência, achar o centro e o raio.
Eu sei que pra uma eq. representar uma circunferência ele deve se encaixar em três condições: os coeficientes de
 e de
e de 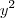 devem existir e devem ser iguais; não pode existir coeficiente para
devem existir e devem ser iguais; não pode existir coeficiente para 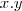 e
e 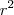 deve ser maior que 0. Na equação
deve ser maior que 0. Na equação  eu achei o
eu achei ocentro (coeficiente de x
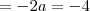 e coeficiente de
e coeficiente de 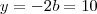 ) mas não sei como achar o raio.
) mas não sei como achar o raio.Eu tenho que passar essa equação para a forma reduzida? Eu não lebro se aprendi a fazer isso no ensino médio. Como posso demonstrar que essa eq. representa uma circunferência?
Na eq.
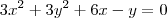 não tem nem termo independente, como se acha o raio disso?
não tem nem termo independente, como se acha o raio disso?MUITO obrigada desde já a quem puder me ajudar!!!
Grande beijo!



