 por willwgo » Qua Jun 29, 2011 16:49
por willwgo » Qua Jun 29, 2011 16:49
(ufmt) o lado, o semiperimetro e a área de um hexágono regular formam,nessa ordem,uma PG. Determine o apótema desse hexágono.
me ajudem...
se conseguirem fazer me digam com chegaram ao resultado..
obrigado
-
willwgo
- Usuário Dedicado

-
- Mensagens: 33
- Registrado em: Qui Fev 17, 2011 15:59
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Molina » Qua Jun 29, 2011 21:50
por Molina » Qua Jun 29, 2011 21:50
Boa noite, will...
Sabemos que um hexágono regular de
lado 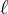
tem
semiperímetro dado por
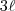
e
área dada por
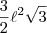
Obs.: Caso tenha alguma dúvida de como eu obtive essas três medidas, avise!
Agora temos a
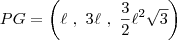
Você precisa agora descobrir o valor de
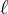
. Para isso use a fórmula de PG, onde diz que o segundo termo dividido pelo segundo termo é igual ao segundo termo dividido pelo primeiro termo. Assim você vai descobrir o valor de
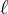
.
O hexágono regular é formado por 6 triângulos equiláteros (usei este fator para descobrir a área dele). O apótema nada mais é do que a altura desses triângulos.
Tente e caso não consiga, avise..
Muito boa a questão, bom estudo!

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por willwgo » Qui Jun 30, 2011 17:31
por willwgo » Qui Jun 30, 2011 17:31
-
willwgo
- Usuário Dedicado

-
- Mensagens: 33
- Registrado em: Qui Fev 17, 2011 15:59
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Molina » Sex Jul 01, 2011 09:13
por Molina » Sex Jul 01, 2011 09:13
Bom dia.
Faça sem aproximações. Quando aparecer raiz não exata, deixe na forma de raiz, veja:
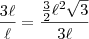
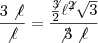
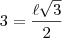
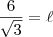
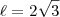
Perceba que este resultado faz sentido, pois temos a
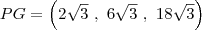
de razão 3.
Agora que você já tem o lado desse hexágono consegues calcular seu apótema?
Caso tenha dúvidas ainda, avise!
Bom estudo,

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por willwgo » Seg Jul 04, 2011 16:50
por willwgo » Seg Jul 04, 2011 16:50
obrigado pela ajuda...

-
willwgo
- Usuário Dedicado

-
- Mensagens: 33
- Registrado em: Qui Fev 17, 2011 15:59
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
Voltar para Geometria Plana
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



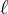 tem semiperímetro dado por
tem semiperímetro dado por 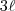 e área dada por
e área dada por 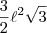
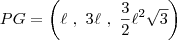
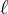 . Para isso use a fórmula de PG, onde diz que o segundo termo dividido pelo segundo termo é igual ao segundo termo dividido pelo primeiro termo. Assim você vai descobrir o valor de
. Para isso use a fórmula de PG, onde diz que o segundo termo dividido pelo segundo termo é igual ao segundo termo dividido pelo primeiro termo. Assim você vai descobrir o valor de 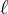 .
.

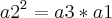
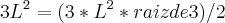
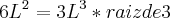
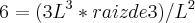
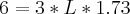
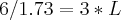
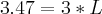
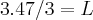
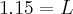

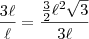
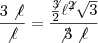
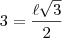
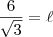
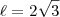
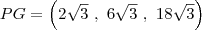 de razão 3.
de razão 3.








