(Unicamp) Sejam A,B,C e D os vértices de um quadrado de lado a= 10cm; Sejam ainda E e F pontos nos lados AD e DC respectivamente, de modo que BEF seja um triângulo equilátero.
a)Qual o comprimento do lado desse triângulo.
b) Calcule a área do mesmo.
Tentativa:
a)Inicialmente fiz as seguintes deduçoes:
AE=CF=y
DE=DF=Z
m seria a altura do triângulo, então m=
![\frac{x.\sqrt[]{3}}{2} \frac{x.\sqrt[]{3}}{2}](/latexrender/pictures/33825d607b3790da3c00bdeebfdaa56e.png)
A soma das áreas dos triângulos ABE, DEF, BCF E BEF é igual a 100cm²
Então,
![[tex]\frac{10.y}{2}+\frac{{z}^{2}}{2}+\frac{10.y}{2}+\frac{x.m}{2} [tex]\frac{10.y}{2}+\frac{{z}^{2}}{2}+\frac{10.y}{2}+\frac{x.m}{2}](/latexrender/pictures/7f97c5f49ec9881a8e090c612dc9e3ca.png) =100.
=100.Resolvendo essa equação, cheguei ao resultado:
x²=
![\frac{100\sqrt[]{3}}{3} \frac{100\sqrt[]{3}}{3}](/latexrender/pictures/ee4c9b8034907608a9c548b7f48e6877.png) .
.Porém no gabarito a resposta é:
a)10(
![\sqrt[]{6}-\sqrt[]{2} \sqrt[]{6}-\sqrt[]{2}](/latexrender/pictures/54a31b3e31784da69f4c24dfb7baa5a3.png) )cm.
)cm.b)100(2
![\sqrt[]{3}-3) \sqrt[]{3}-3)](/latexrender/pictures/122d6d8440180c126b70880235409ad7.png) cm².
cm².Onde foi que eu errei?


 )
)
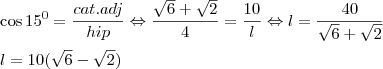




 .
.



