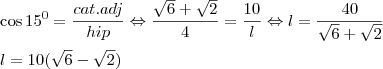por Mi_chelle » Qua Mai 04, 2011 20:16
por Mi_chelle » Qua Mai 04, 2011 20:16
Não estou conseguindo resolver a seguinte questão:
(Unicamp) Sejam A,B,C e D os vértices de um quadrado de lado a= 10cm; Sejam ainda E e F pontos nos lados AD e DC respectivamente, de modo que BEF seja um triângulo equilátero.
a)Qual o comprimento do lado desse triângulo.
b) Calcule a área do mesmo.
Tentativa:
a)Inicialmente fiz as seguintes deduçoes:
AE=CF=y
DE=DF=Z
m seria a altura do triângulo, então m=
![\frac{x.\sqrt[]{3}}{2} \frac{x.\sqrt[]{3}}{2}](/latexrender/pictures/33825d607b3790da3c00bdeebfdaa56e.png)
A soma das áreas dos triângulos ABE, DEF, BCF E BEF é igual a 100cm²
Então,
![[tex]\frac{10.y}{2}+\frac{{z}^{2}}{2}+\frac{10.y}{2}+\frac{x.m}{2} [tex]\frac{10.y}{2}+\frac{{z}^{2}}{2}+\frac{10.y}{2}+\frac{x.m}{2}](/latexrender/pictures/7f97c5f49ec9881a8e090c612dc9e3ca.png)
=100.
Resolvendo essa equação, cheguei ao resultado:
x²=
![\frac{100\sqrt[]{3}}{3} \frac{100\sqrt[]{3}}{3}](/latexrender/pictures/ee4c9b8034907608a9c548b7f48e6877.png)
.
Porém no gabarito a resposta é:
a)10(
![\sqrt[]{6}-\sqrt[]{2} \sqrt[]{6}-\sqrt[]{2}](/latexrender/pictures/54a31b3e31784da69f4c24dfb7baa5a3.png)
)cm.
b)100(2
![\sqrt[]{3}-3) \sqrt[]{3}-3)](/latexrender/pictures/122d6d8440180c126b70880235409ad7.png)
cm².
Onde foi que eu errei?
-
Mi_chelle
- Usuário Ativo

-
- Mensagens: 21
- Registrado em: Seg Mar 28, 2011 17:35
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Tec. Química
- Andamento: formado
 por claudinho » Ter Jun 14, 2011 22:52
por claudinho » Ter Jun 14, 2011 22:52
No Vértice B, alem do angulo do triangulo equilatero (60°)
temos 02 angulos que medem 30/2 <=> 15° cada
peguemos um dos triangulos, BEC por exemplo, onde:
BC = 10 cm (lado do quadradro)
BE = hipotenusa ( tb é o lado do triangulo equilatero a ser descoberto)
C = 90°
E = 75°
B = 15°
Lembrando a "subtração de cosseno" :
(eu ja tinha sacado q esta formula salvaria a questao, mas confesso q tive q relembra-la pelo google,

)

Agora podemos trabalhar com o triangulo BEC e descobrir BE (chamemos de "
l")
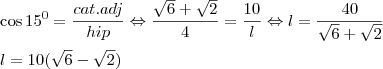
Solucionando assim sua questão "a", identico ao seu gabarito
Para questão "b" tem q usar a "fórmula da Area do triangulo equilatero"

fiz aqui "no papel" e bateu tb identico ao seu gabarito,
(perdao por nao resolucinar aqui por enquanto no tex)
Abraços
-
claudinho
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Sex Jun 10, 2011 13:55
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por FilipeCaceres » Ter Jun 14, 2011 23:41
por FilipeCaceres » Ter Jun 14, 2011 23:41
Está questão já foi resolvida, veja
viewtopic.php?f=119&t=4631&p=15424Abraço.
-
FilipeCaceres
- Colaborador Voluntário

-
- Mensagens: 351
- Registrado em: Dom Out 31, 2010 21:43
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Tec. Mecatrônica
- Andamento: formado
Voltar para Geometria Plana
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Razão da área do triângulo para a área do quadrilátero]
 por Mayra Luna » Sex Nov 23, 2012 20:17
por Mayra Luna » Sex Nov 23, 2012 20:17
- 2 Respostas
- 4411 Exibições
- Última mensagem por Mayra Luna

Ter Nov 27, 2012 14:53
Geometria Plana
-
- [Área] Área de triangulo e trapézio
 por smlspirit » Qui Jul 19, 2012 20:07
por smlspirit » Qui Jul 19, 2012 20:07
- 1 Respostas
- 2995 Exibições
- Última mensagem por e8group

Qui Jul 19, 2012 20:57
Geometria Plana
-
- Área do Triângulo
por Padoan » Qui Fev 11, 2010 18:36
- 6 Respostas
- 8365 Exibições
- Última mensagem por MarceloFantini

Sex Fev 12, 2010 13:42
Geometria Plana
-
- Área do Triângulo
por Cleyson007 » Sex Mai 14, 2010 13:07
- 1 Respostas
- 2324 Exibições
- Última mensagem por Douglasm

Sex Mai 14, 2010 13:38
Geometria Analítica
-
- Área do Triângulo
por valeuleo » Ter Abr 05, 2011 11:25
- 1 Respostas
- 2690 Exibições
- Última mensagem por LuizAquino

Ter Abr 05, 2011 11:42
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\frac{x.\sqrt[]{3}}{2} \frac{x.\sqrt[]{3}}{2}](/latexrender/pictures/33825d607b3790da3c00bdeebfdaa56e.png)
![[tex]\frac{10.y}{2}+\frac{{z}^{2}}{2}+\frac{10.y}{2}+\frac{x.m}{2} [tex]\frac{10.y}{2}+\frac{{z}^{2}}{2}+\frac{10.y}{2}+\frac{x.m}{2}](/latexrender/pictures/7f97c5f49ec9881a8e090c612dc9e3ca.png) =100.
=100.![\frac{100\sqrt[]{3}}{3} \frac{100\sqrt[]{3}}{3}](/latexrender/pictures/ee4c9b8034907608a9c548b7f48e6877.png) .
.![\sqrt[]{6}-\sqrt[]{2} \sqrt[]{6}-\sqrt[]{2}](/latexrender/pictures/54a31b3e31784da69f4c24dfb7baa5a3.png) )cm.
)cm.![\sqrt[]{3}-3) \sqrt[]{3}-3)](/latexrender/pictures/122d6d8440180c126b70880235409ad7.png) cm².
cm².

 )
)