 por maria cleide » Sáb Mai 28, 2011 16:49
por maria cleide » Sáb Mai 28, 2011 16:49
O perímetro de um triângulo ABC é igual a 45cm. A bissetriz interna do ângulo  divide o lado oposto em dois segmentos de medidas iguais a 10cm e 8cm. Qual a medida do menor lado desse triângulo?
A-( ) 10cm
B-( ) 11cm
C-( ) 12cm
D-( ) 14cm
Só sei que o lado maior é o que mede 18cm, mas não consigo desenvolver o problema.
-
maria cleide
- Usuário Parceiro

-
- Mensagens: 54
- Registrado em: Dom Mai 08, 2011 12:57
- Formação Escolar: ENSINO FUNDAMENTAL I
- Andamento: cursando
 por MarceloFantini » Sáb Mai 28, 2011 17:55
por MarceloFantini » Sáb Mai 28, 2011 17:55
Se a bissetriz divide o lado oposto em segmentos de medidas iguais a 10 cm e 8 cm, respectivamente, então temos que os lados correspondentes são proporcionais a eles, logo:
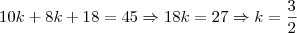
. Portanto o menor lado é

. Resposta C.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por maria cleide » Dom Mai 29, 2011 19:42
por maria cleide » Dom Mai 29, 2011 19:42
Não entendi porque você chegou na conclusão que os lados correspondentes são proporcionais e que os valores destes lados são

e

.
-
maria cleide
- Usuário Parceiro

-
- Mensagens: 54
- Registrado em: Dom Mai 08, 2011 12:57
- Formação Escolar: ENSINO FUNDAMENTAL I
- Andamento: cursando
 por MarceloFantini » Dom Mai 29, 2011 19:55
por MarceloFantini » Dom Mai 29, 2011 19:55
Putz Maria, eu me lembro que existe um teorema chamado teorema das bissetrizes que diz isso, mas não me lembro a demonstração. Procure por ele. Peço desculpas por acabar jogando isso, mas tenho certeza que é assim.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Geometria Plana
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Perímetro do triângulo
por leticiadelduque » Dom Ago 21, 2011 12:02
- 2 Respostas
- 1735 Exibições
- Última mensagem por leticiadelduque

Dom Ago 21, 2011 17:02
Geometria Plana
-
- [Perímetro do Triângulo]
 por Mayra Luna » Qui Out 11, 2012 23:03
por Mayra Luna » Qui Out 11, 2012 23:03
- 4 Respostas
- 2194 Exibições
- Última mensagem por Mayra Luna

Sex Out 12, 2012 17:25
Geometria Plana
-
- Duvida em perimetro de triangulo
 por bmachado » Dom Mar 18, 2012 17:39
por bmachado » Dom Mar 18, 2012 17:39
- 2 Respostas
- 3917 Exibições
- Última mensagem por bmachado

Seg Mar 19, 2012 16:21
Geometria Plana
-
- Calculo de perimetro do triangulo retangulo
por Marcinha » Dom Nov 13, 2011 16:12
- 1 Respostas
- 2967 Exibições
- Última mensagem por Andreza

Dom Nov 13, 2011 18:08
Geometria Plana
-
- Triangulo e quadrado, perimetro constante
 por heldersmd » Sáb Set 15, 2012 12:42
por heldersmd » Sáb Set 15, 2012 12:42
- 1 Respostas
- 1504 Exibições
- Última mensagem por young_jedi

Sáb Set 15, 2012 14:54
Geometria Plana
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


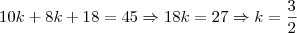 . Portanto o menor lado é
. Portanto o menor lado é  . Resposta C.
. Resposta C.

 e
e  .
.