eu gostaria d saber como pensar sobre essa kestão:
"Oretângulo abaixo de dimensões
 e
e  está decomposto em quatro quadrados, como mostra figura. Calcule o valor da razão
está decomposto em quatro quadrados, como mostra figura. Calcule o valor da razão  ."
."bom, eu tentei fazer pelas áreas dos quarados e não deu certo:

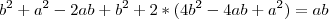
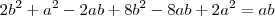
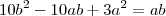
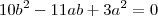
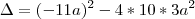


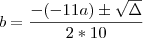


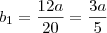



No gabarito, diz q a resposta é a primeira. Porque não pode ser a segunda?




![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)