 por fernandocez » Seg Fev 14, 2011 17:21
por fernandocez » Seg Fev 14, 2011 17:21
Oi pessoal, mais uma que eu não consigo resolver. Essa é do concurso para magistério 2007. Eu fiz licenciatura em matemática mas acho que sou muito fraco. Preciso estudar muito pra passar no concurso.
O segmento AB é uma corda de uma circunferência de centro O. Prolongando AB de um comprimento BC igual ao raio da circunferência, verifica-se que o ângulo BCO mede 24º. Então, o ângulo AOC mede:
Eu fiz o seguinte: fiz um circulo, tracei a corda AB fiz o prolongamento BC igual ao raio. Tracei do centro O até ponto A e tracei até o ponto C. Apareceu um triangulo AOC. Nesse triangulo tem um ângulo de 24º em C e mais dois x+y=156, x+y+24=180º, ok? Agora eu não consigo continuar. Agradeço quem puder ajudar.
-

fernandocez
- Colaborador Voluntário

-
- Mensagens: 131
- Registrado em: Seg Fev 14, 2011 15:01
- Localização: São João de Meriti - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matemática
- Andamento: formado
 por LuizAquino » Seg Fev 14, 2011 19:57
por LuizAquino » Seg Fev 14, 2011 19:57
A figura abaixo ilustra o exercício.

- circunferencia.png (35.58 KiB) Exibido 1410 vezes
Note que os triângulos AOB e OBC são isósceles. Além disso, temos que
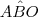
é um ângulo externo do triângulo OBC. Sendo assim,

e ambos medem 24°;

e ambos medem 48°.
Do triângulo AOC temos que
(x+24°)+48º+24°=180°, de onde obtemos que
x=84°. Portanto, o ângulo AÔC mede 108°.
fernandocez escreveu:Preciso estudar muito pra passar no concurso.
Para revisar os conteúdos do ensino fundamental e médio, indico para você os vídeos do Nerckie no YouTube:
http://www.youtube.com/nerckie
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Geometria Plana
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Questão prova magisterio 2008
por fernandocez » Seg Fev 14, 2011 16:42
- 4 Respostas
- 3031 Exibições
- Última mensagem por LuizAquino

Ter Fev 15, 2011 20:10
Polinômios
-
- Questão prova magisterio 2008
 por fernandocez » Sáb Fev 26, 2011 11:39
por fernandocez » Sáb Fev 26, 2011 11:39
- 3 Respostas
- 2396 Exibições
- Última mensagem por LuizAquino

Sáb Fev 26, 2011 19:15
Geometria Plana
-
- [trigonometria] concurso magistério 2007 (33)
por fernandocez » Sex Dez 20, 2013 09:27
- 2 Respostas
- 1959 Exibições
- Última mensagem por fernandocez

Sáb Dez 21, 2013 16:38
Trigonometria
-
- PG prova concurso estado magistério 2008
por fernandocez » Sex Fev 25, 2011 20:23
- 3 Respostas
- 2325 Exibições
- Última mensagem por Molina

Sáb Fev 26, 2011 13:08
Progressões
-
- [Geometria plana] prova magistério 2011
 por fernandocez » Sex Nov 23, 2012 15:54
por fernandocez » Sex Nov 23, 2012 15:54
- 4 Respostas
- 3575 Exibições
- Última mensagem por fernandocez

Sáb Nov 24, 2012 16:17
Geometria Plana
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


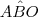 é um ângulo externo do triângulo OBC. Sendo assim,
é um ângulo externo do triângulo OBC. Sendo assim,  e ambos medem 24°;
e ambos medem 24°;  e ambos medem 48°.
e ambos medem 48°.