 por nerabil » Seg Jan 03, 2011 21:03
por nerabil » Seg Jan 03, 2011 21:03
Olá Mestres, um abençoado 2011 a todos!
Tenho o seguinte problema:
Preciso encontrar o ângulo

ou o ângulo

, para aplicar a função ArcTangente e obter o ponto A(x,y) pelos senos e cossenos...
Dados os pontos C e B, e o cateto b desejo obter o ponto A de modo que obtenha um triângulo retângulo.
o Ponto D obtenho facilmente pelos seno e cosseno dos ângulos obtidos pela função ArcTangente dos pontos C e B.
A distância do cateto "b" sempre será igual (valor fixo), mas a hipotenusa "a" é variável, bem como os pontos B e C tornando meu angulo

sempre variável.
desde já agradeço...
- Anexos
-

- Triângulo ArcTan.png (5.05 KiB) Exibido 2699 vezes
-
nerabil
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Seg Jan 03, 2011 12:00
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Tecnólogo Processamento de dados
- Andamento: formado
 por MarceloFantini » Ter Jan 04, 2011 10:52
por MarceloFantini » Ter Jan 04, 2011 10:52
Bom, basta pegar traçar uma reta que passa por C e que seja tangente a circunferência de centro em B e raio b. O triângulo formado será sempre retângulo.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por nerabil » Ter Jan 11, 2011 03:50
por nerabil » Ter Jan 11, 2011 03:50
ok, como chego no ângulo
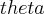
ou

, ou ainda como chego no ponto A(x,y), seja apartir da equação da circunferência ou outro meio?
Terei que programar essa função para descobrir o A(x,y). Imagino que terei que fazer iterações com cada um dos pontos da circunferência testando se a reta CA é tangênte à circunferência.
É esta minha questão, não vou traçar uma reta manualmente para tangenciar a circunferência, preciso dos meios para achar ponto A(x,y) ou ainda o ângulo
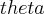
ou

.
-
nerabil
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Seg Jan 03, 2011 12:00
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Tecnólogo Processamento de dados
- Andamento: formado
 por MarceloFantini » Ter Jan 11, 2011 11:42
por MarceloFantini » Ter Jan 11, 2011 11:42
Provavelmente não vai ajudar, mas
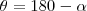
. E sim, não sei muito de programação mas testar se a reta CA é tangente deve ser um meio, só que talvez isso mude o problema pra quantidade de memória.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Renato_RJ » Ter Jan 11, 2011 15:47
por Renato_RJ » Ter Jan 11, 2011 15:47
Tira uma dúvida, o ponto D está na mesma reta que os pontos B e C ?? Se sim, já pensou em prolongar a reta AC até um ponto E perpendicular ao ponto D e, com isso, você teria dois triângulos semelhantes, o triângulo DEC e o triângulo BAC, logo o ângulo alfa sairia por semelhança.
Grato,
Renato.
Iniciando a minha "caminhada" pela matemática agora... Tenho muito o quê aprender...
-

Renato_RJ
- Colaborador Voluntário

-
- Mensagens: 306
- Registrado em: Qui Jan 06, 2011 15:47
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado em Matemática
- Andamento: cursando
Voltar para Geometria Plana
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Derivada num ponto pela definição
por emsbp » Sex Jul 13, 2012 16:52
- 1 Respostas
- 1572 Exibições
- Última mensagem por Russman

Sex Jul 13, 2012 18:09
Cálculo: Limites, Derivadas e Integrais
-
- Função real definida pela soma de uma função par c/uma ímpar
por Taah » Sáb Mar 27, 2010 15:33
- 3 Respostas
- 5571 Exibições
- Última mensagem por Taah

Dom Mar 28, 2010 13:21
Funções
-
- Determunar a área limitada pela parábola y= x²+1 e pela reta
por lucat28 » Ter Ago 30, 2011 19:32
- 2 Respostas
- 5100 Exibições
- Última mensagem por lucat28

Dom Set 04, 2011 11:45
Cálculo: Limites, Derivadas e Integrais
-
- Achar catetos pela hipotenusa e pela altura
 por gustavoluiss » Dom Dez 05, 2010 23:44
por gustavoluiss » Dom Dez 05, 2010 23:44
- 5 Respostas
- 8617 Exibições
- Última mensagem por gustavoluiss

Seg Dez 06, 2010 20:37
Geometria Plana
-
- Encontrar a Função Matemática
por Marcos RS » Sex Set 04, 2009 00:46
- 3 Respostas
- 2518 Exibições
- Última mensagem por Marcos RS

Ter Set 08, 2009 20:25
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 ou o ângulo
ou o ângulo  , para aplicar a função ArcTangente e obter o ponto A(x,y) pelos senos e cossenos...
, para aplicar a função ArcTangente e obter o ponto A(x,y) pelos senos e cossenos... sempre variável.
sempre variável.



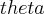 ou
ou 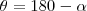 . E sim, não sei muito de programação mas testar se a reta CA é tangente deve ser um meio, só que talvez isso mude o problema pra quantidade de memória.
. E sim, não sei muito de programação mas testar se a reta CA é tangente deve ser um meio, só que talvez isso mude o problema pra quantidade de memória.


 substitui-se
substitui-se 
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.