 por victoreis1 » Sex Nov 19, 2010 14:20
por victoreis1 » Sex Nov 19, 2010 14:20
Tou um pouco sem tempo, mas direi como eu calcularia isso:
Seja O o centro da circunferência menor, que coincide com o centro do quadrado, e 'o' o centro de uma das circunferências maiores. Calcule a distância de O até 'o', usando geometria analítica básica, depois subtraia dessa distância o raio de uma circunferência maior (igual à metade do lado do quadrado). Então restará somente o raio da circunferência menor, use a fórmula da área de uma circunferência e acabou-se o problema..
tomara que tenha dado pra entender
-
victoreis1
- Usuário Dedicado

-
- Mensagens: 37
- Registrado em: Qua Out 20, 2010 14:49
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Pedro123 » Sex Nov 19, 2010 15:43
por Pedro123 » Sex Nov 19, 2010 15:43
Fala meu amigo, como não sei usar esse Latex muito bem, fiz uma resolução ao meu jeito ta ai abrass
qualquer duvida pergunte
- Anexos
-
[O anexo não pode ser exibido, pois a extensão doc foi desativada pelo administrador.]
-
Pedro123
- Usuário Parceiro

-
- Mensagens: 60
- Registrado em: Qui Jun 10, 2010 22:46
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Mecanica - 1° Período
- Andamento: cursando
 por alexandre32100 » Sex Nov 19, 2010 15:52
por alexandre32100 » Sex Nov 19, 2010 15:52
O raio de cada circunferência maior é

, chamarei de

o raio da cincunferência menor.

- figura.png (40.97 KiB) Exibido 4240 vezes
Por Pitágoras:


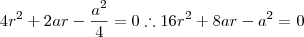
Aplicando Bhaskara, Báskara ou Báscara chegamos a
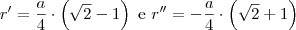
. Podemos descartar
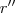
, pois, com

positivo, esta raiz assume valor negativo.
Concluímos que
![r=\dfrac{a}{4}\cdot\left(\sqrt{2}-1\right)
Por fim
[tex]\\A_{\circ}=\pi r^2=\pi\cdot\dfrac{a^2}{16}\cdot(\sqrt{2}-1)^2=\dfrac{(3-2\sqrt{2})a^2\pi}{16} r=\dfrac{a}{4}\cdot\left(\sqrt{2}-1\right)
Por fim
[tex]\\A_{\circ}=\pi r^2=\pi\cdot\dfrac{a^2}{16}\cdot(\sqrt{2}-1)^2=\dfrac{(3-2\sqrt{2})a^2\pi}{16}](/latexrender/pictures/a199430f6b6b62ba51a0b29a8c0857c3.png)
-
alexandre32100
-
 por Balanar » Sex Nov 19, 2010 15:56
por Balanar » Sex Nov 19, 2010 15:56
Perfeito obrigado a todos.

-
Balanar
- Usuário Parceiro

-
- Mensagens: 72
- Registrado em: Qua Dez 03, 2008 07:18
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Pedro123 » Sex Nov 19, 2010 16:01
por Pedro123 » Sex Nov 19, 2010 16:01
kkkkkkkkkk é alexandre, essa também é minha duvida... Bhaskara, baskara báskara ou bascara? kkkkkk
-
Pedro123
- Usuário Parceiro

-
- Mensagens: 60
- Registrado em: Qui Jun 10, 2010 22:46
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Mecanica - 1° Período
- Andamento: cursando
Voltar para Geometria Plana
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Área Sombreada
por Balanar » Sáb Nov 13, 2010 22:37
- 1 Respostas
- 2484 Exibições
- Última mensagem por Jefferson

Qui Nov 18, 2010 12:58
Geometria Plana
-
- Área Sombreada-2
por Balanar » Sex Nov 19, 2010 16:55
- 2 Respostas
- 2015 Exibições
- Última mensagem por Rogerio Murcila

Sex Nov 19, 2010 18:02
Geometria Plana
-
- Área Sombreada-3
por Balanar » Sex Nov 19, 2010 18:13
- 1 Respostas
- 1703 Exibições
- Última mensagem por MarceloFantini

Sex Nov 19, 2010 18:21
Geometria Plana
-
- Qual é em cm ² a área sombreada
por leticiapires52 » Ter Abr 08, 2014 11:28
- 2 Respostas
- 1925 Exibições
- Última mensagem por Russman

Qua Abr 09, 2014 23:51
Geometria Plana
-
- [Razão da área do triângulo para a área do quadrilátero]
 por Mayra Luna » Sex Nov 23, 2012 20:17
por Mayra Luna » Sex Nov 23, 2012 20:17
- 2 Respostas
- 4412 Exibições
- Última mensagem por Mayra Luna

Ter Nov 27, 2012 14:53
Geometria Plana
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.








 , chamarei de
, chamarei de  o raio da cincunferência menor.
o raio da cincunferência menor.

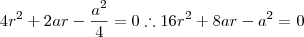
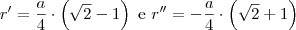 . Podemos descartar
. Podemos descartar  , pois, com
, pois, com  positivo, esta raiz assume valor negativo.
positivo, esta raiz assume valor negativo.![r=\dfrac{a}{4}\cdot\left(\sqrt{2}-1\right)
Por fim
[tex]\\A_{\circ}=\pi r^2=\pi\cdot\dfrac{a^2}{16}\cdot(\sqrt{2}-1)^2=\dfrac{(3-2\sqrt{2})a^2\pi}{16} r=\dfrac{a}{4}\cdot\left(\sqrt{2}-1\right)
Por fim
[tex]\\A_{\circ}=\pi r^2=\pi\cdot\dfrac{a^2}{16}\cdot(\sqrt{2}-1)^2=\dfrac{(3-2\sqrt{2})a^2\pi}{16}](/latexrender/pictures/a199430f6b6b62ba51a0b29a8c0857c3.png)


